Six Numbers, Two Inequalities
Problem
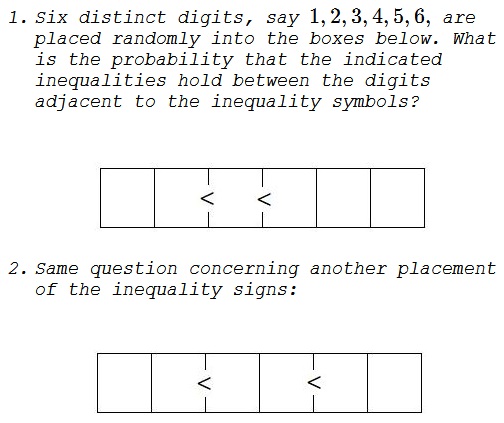
Solution
Unlike the previous problem, the two questions have different answers.
For both questions, the sample space counts $6!$ elements. The task is to count how many of these satisfy both inequalities. What is important is how many combinations of the numbers adjacent to the inequality symbols satisfy the inequalities. For the first question we multiply that number by $3!$ to account for the remaining three digits. For the second question the factor is $2!$
For the first question, if the first number is $1,$ there are $10$ choices for the other two: $(2,3),$ $(2,4),$ $(2,5),$ $(2,6),$ $(3,4),$ $(3,5),$ $(3,6),$ $(4,5),$ $(4,6),$ $(5,5).$ Similarly, if the first number is $2,$ there are six variants for the other two numbers. Then there are three variants if the first number is $3$ and only one if the first number if $4.$ In all there are $(10+6+3+1)\cdot 3!$ combinations that satisfy both inequalities. The probability of this happening is $\displaystyle \frac{20\cdot 3!}{6!}=\frac{1}{6}.$
Leon Stein (Boca Raton, FL) suggested the following argument: for any triplet there are $6$ ways to put them in $3$ spots, but only one holds ordering, thus only $\displaystyle \frac{1}{6}$ of total arrangements is valid.
For the second question, there are ${6 \choose 4}$ ways to fill the slots around the inequality symbols. For every choice of the four numbers there are $6$ ways to satisfy the two inequalities, e.g., $(1,2,3,4),$ $(1,3,2,4),$ $(1,4,2,3),$ $(2,3,1,4),$ $(2,4,1,3),$ $(3,4,1,2).$ Thus the total number of "successful" combinations is ${6 \choose 4}\cdot 6\cdot 2,$ giving the sought probability as $\displaystyle \frac{6\cdot 5\cdot 6\cdot 2}{2\cdot 6!}=\frac{1}{4}.$
Finally, for the second question, Long Huynh Huu has observed that the two inequalties are independent because swapping the digits in one pair does not affect the other. Thus, borrowing from the logic of the first problem, the answer is $\displaystyle \frac{1}{2}\times\frac{1}{2}=\frac{1}{4}.$
Acknowledgment
These problems have been inspired by Donald Knuth's puzzles from the multi-author collection Puzzle Box, v 2.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73578385
