Quotient Estimates II
Problem
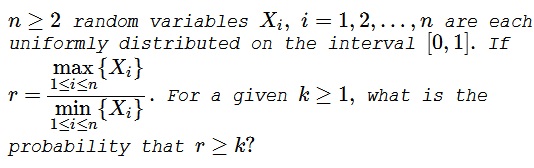
Solution 1
Let $\displaystyle U=\min_{1\le i\le n}\{X_i\},$ $\displaystyle V=\max_{1\le i\le n}\{X_i\}.$ The question is to find $\displaystyle P(V\ge kU),$ $k\ge 1.$
To solve the problem we have to integrated the joint distribution $f_{U,V}(u,v)$ over the shaded triangle. The triangle is a part of the region $\{(u,v):\,u\lt v\}.$ Thus, we only need to find $f_{U,V}(u,v)$ for $u\lt v.$
Let $f(x)$ be the uniform density function on $[0,1].$ For all $i=1,\ldots,n,$ $f_{X_i}(x)=f(x).$ Let $F(x)$ be the uniform distribution function: $\displaystyle F(x)=\int_{-\infty}^xf(\xi)d\xi:$
$F(x)=\begin{cases} 0,&x\le 0,\\ x,&0\le x\le 1,\\ 1,&x\ge 1.\end{cases}$
For all $i=1,\ldots,n,$ $F_{X_i}(x)=F(x).$ Now, since $X_1,\ldots,X_n$ are independent,
$\begin{align}F_V(v)=P(V\lt v)&=P(X_1\lt v)P(X_2\lt v)\cdots P(X_n\lt v)\\ &=F_{X_1}(v)F_{X_2}(v)\cdots F_{X_n}(v)=F^n(v). \end{align}$
so that
$F_V(v)=\begin{cases} 0,&v\le 0,\\ v^n,&0\le v\le 1,\\ 1,&v\ge 1.\end{cases}$
For the cdf,
$\begin{align}F_{U,V}(u,v)&=P(U\le u, V\le v)\\ &=P(U\le u,X_1\le v,X_2\le v,\ldots,X_n\le v). \end{align}$
To remind, $U\gt u,$ iff for all $i=1,\ldots,n,$ $X_i\gt u.$ $U\le u$ means the opposite, i.e., that $X_i\le u$ for some $X_i.$ So we may continue (with $u\lt v)$
$\begin{align}F_{U,V}(u,v)&=P(U\le u, V\le v)\\ &=P(U\le u,X_1\le v,X_2\le v,\ldots,X_n\le v)\\ &=P(X_1\le v,X_2\le v,\ldots,X_n\le v)-\prod_{i=1}^nP(u\lt X_i\le v)\\ &=F^n(v)-P(u\lt X_1\le v)P(u\lt X_2\le v)\cdots)P(u\lt X_n\le v)\\ &=F^n(v)-(F(v)-F(u))^n\\ &=v^n-(v-u)^n. \end{align}$
Next, $\displaystyle f_{U,V}(u,v)=\frac{\partial^2F_{U,V}(u,v)}{\partial u\partial v}=n(n-1)(v-u)^{n-2}.$ So, finally,
$\displaystyle\begin{align}P(V\gt kU)&=\int_{0}^1\int_0^{v/k}n(n-1)(v-u)^{n-2}dudv\\ &=\int_{0}^1n(v-u)^{n-1}\big|^0_{v/k}dudv\\ &=\int_0^1n\left(v^{n-1}-v^{n-1}\left(1-\frac{1}{k}\right)^{n-1}\right)dv\\ &=\int_0^1n\left(v^{n-1}-\left(v-\frac{v}{k}\right)^{n-1}\right)dv\\ &=\int_0^1n\left(v^{n-1}-v^{n-1}\left(1-\frac{1}{k}\right)^{n-1}\right)dv\\ &=\int_0^1nv^{n-1}\left(1-\left(1-\frac{1}{k}\right)^{n-1}\right)dv\\ &=1-\left(1-\frac{1}{k}\right)^{n-1}. \end{align}$
Solution 2
Let $x$ and $y$ be the smallest and largest of the chosen numbers. These numbers are shown on the $X$ and $Y$ axes in the figure below. The red region is not feasible as $y>x$. The region where the ratio is less than $k$ is the green region.
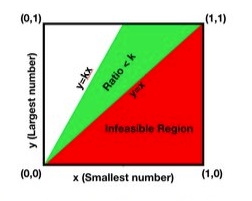
The probability density of the chosen set of points being in a window $dxdy$ around $(x,y)$ is
$f(x,y)dxdy = n(n-1)(y-x)^{n-2}dxdy.$
The $(y-x)^{n-2}$ is the probability of choosing the $(n-2)$ points between the two fixed end points. The $n(n-1)$ comes from the choice of choosing the end points.
The required probability is one minus the integral of this density over the green region and is given by
$\displaystyle \begin{align} P&=1-\int_{y=0}^{1}\int_{x=\frac{y}{k}}^{y} f(x,y)dxdy =1-\int_{y=0}^{1}\int_{x=\frac{y}{k}}^{y} n(n-1)(y-x)^{n-2}dxdy \\ &=1-\int_{y=0}^{1} ny^{n-1}\left[\left(1-\frac{1}{k}\right)^{n-1}\right]dy \\ &=1-\left(1-\frac{1}{k}\right)^{n-1}. \end{align}$
Solution 3
We consider
$\displaystyle r=\frac{\max\limits_{1 \leq i \leq n}\{X_i\}}{\min\limits_{1 \leq i \leq n}\{X_i\}}= \max\limits_{0 \leq i \neq j \leq n} \frac{X_i}{X_j}$
We know the distribution of $\displaystyle \omega=\frac{X_i}{X_j}$ and can arrange $m$ permutations, with $\displaystyle m=\frac{n!}{(n-2)!}$. If you assume that $n-1$, ratios are independent, with pdf $\displaystyle f_\omega(\omega)=\frac{1}{2\omega^2}$ and cdf $\displaystyle F_\omega(\omega)=\frac{1}{2\omega}$, then:
$\displaystyle \mathbb{P}(\max \{\omega_1, \omega_2, \ldots, \omega_m\}>k)= 1-\left(1-\frac{1}{ k}\right)^{n-1}, \;k \geq 1$
Acknowledgment
The problem is from P. J. Nahin's Will You Be Alive 10 Years from Now? (Princeton University Press, 2014).
Solution 1 is my adaptation of Nahin's solution; Solution 2 is by Amit Itagi; Solution 3 is by N. N. Taleb.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73571207
