Lucky Times at a Moscow Math Olympiad
Problem

Solution to part 1
For a moment defined as $h:m:s$ consider the moment $11-h:59-m:60-s.$ The two constitute the reflections of each other in the vertical diameter (the line 12-6).
For example, $7:42:12$ reflects into $4:17:48.$ The latter is lucky, the former is not.
In general, a legitimate position of the three hands, reflects into another legitimate position. However, one is lucky, the other is not. It follows that there is a 1-1 correspondence between lucky and unlucky moments. More than that two discrete successive lucky moments, like say, $h:m:s$ and $h:m:s+1$ correspond to two successive unlucky moments $11-h: 59-m:60-s-1$ and $11-h: 59-m:60-s$. Thus the two define one-second intervals, corresponding to each other; though one is entirely lucky, the other entirely unlucky. The argument cold be expanded to intervals longer than one second. So, in general, the reflection of a lucky interval is an unlucky interval of the same length, making the two events equiprobable: the probability of each is $\displaystyle \frac{1}{2}.$
Solution 1 to part 2
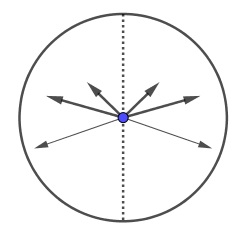
Consider any two hands, e.g., the hour and the minute ones and the clock face sector formed by their extensions across the center of the face:

Whenever the second hand falls into that sector, the moment is unlucky; a moment is lucky if the second hand falls outside the sector.
We can simulate the situation with two random points on the circle. Two points split the circle into two arcs and it appears that we are interested in their relative length: the unlucky sector is never bigger than $180^{\circ}.$
Cut the circle at one of the points. The result is a segment with a random point inside. The point divides the segment into two pieces. In an earlier problem (Three Random Points on a Circle) we found that the the average length of the longer piece is $\displaystyle \frac{3}{4}$ of the whole segment, while that of the shorter piece is $\displaystyle \frac{1}{3}.$
Back to the original problem, the lucky moments of a day come up with the probability of $\displaystyle \frac{3}{4},$ three times more often than the unlucky moments.
There's a lingering question about the selection of two points. Clearly, not any to positions of the hour and minute hands correspond to a real time moment. To resolve that, we cut the circle at the hour point and drop two other hands randomly. Then the situation is exactly like that in dropping one point on a segment.
Solution 2 to part 2
For angle $\theta$ between the hour and minute hands, its unlucky only if second hand is in the diametrically opposite sector of angle $\theta.$ So, its lucky over $2\pi-\theta$ out of $2\pi.$ So,
$\displaystyle P(lucky) = \int_0^{\pi}\frac{2\pi-\theta}{2\pi} d(\theta) / \pi = \frac{3}{4}.$
Solution 3 to part 2
In fact, the integration does not even seem necessary: based on the argument above,
- When hour and min hands are closest, $P(lucky)=1$
- When hour and min hands are farthest, $\displaystyle P(lucky)=\frac{1}{2}.$
So, $P(lucky)$ for all hour and minute hands positions is $\displaystyle \frac{1}{2}\left(1 + \frac{1}{2}\right) = \frac{3}{4}.$
Acknowledgment
The problem is based on two entries at the Moscow Mathematical Olympiad: 1993/A4 and 1994/A5, see Moscow Mathematical Olympiads, 1993-1999 by R. Fedorov, A. Belov, A. Kovaldzhi, I. Ivashchenko (MSRI/AMS, 2011).
Solutions 2 and 3 are by Thamizh Kudimagan.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73561696
