Outline Mathematics
Geometry
Three Touching Circles
Consider the following problem:
Three circles S1, S2 and S3, touch pairwise in three distinct points. Show that the lines joining the point of tangency of S1 and S2 cross S3 again in points collinear with the center of S3, i.e., forming its diameter.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyThree circles S1, S2 and S3, touch pairwise in three distinct points. Show that the lines joining the point of tangency of S1 and S2 cross S3 again in points collinear with the center of S3, i.e., forming its diameter.
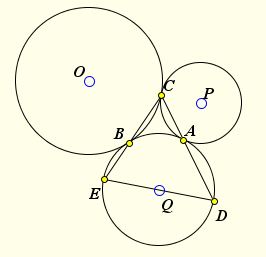
Let O, P, Q be the centers of circles S1, S2 and S3, respectively. Denote the tangency points of S2 and S3, S1 and S3, S1 and S2 as A, B, C. And, finally, let, D be the point of intersection of AC with S3 other than A, and E the point of intersection of BC with S3 other than B.
We know that CP||DQ,DQ,CO,BC and CO,DQ,CO,BC||EQ. But O, C, P are collinear,common,distant,collinear. Therefore, D, Q, E are also collinear. It follows that DE is a diameter of S3.
Note that the statement holds both for external and internal tangency. In the latter case, the statement appears directly related to Lemma 1 from Archimedes' Book of Lemmas. Indeed, the significance of the role played by the tangency point C becomes transparent with an observation that it lies on common line of two diameters of two circles.
(The terms you met: Collinear points, Diameter of a circle)
References
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580073
