Construct a line tangent to two given circles

A circle is a locus of points equividistant from a given point, the center of the circle. The common distance to the center is known as the radius of the circle. The smaller the radius the smaller the circle. For the radius equal to zero the circle shrinks to a point - its own center. It's the only point located at the distance 0 from the center. Therefore, technically speaking, the following problem is a special case of the original one.

Construct a line through a given point tangent to a given circle.

An Aside

This problem can be solved with the compass alone without help of a ruler.

What I want to establish is that the two problems are actually equivalent. Once you know how to solve the second (apparently the simpler) one, you would be able to solve the first one as well. The following diagrams demonstrate that this is indeed so both for internal and external tangents.

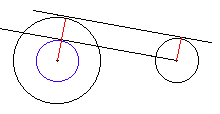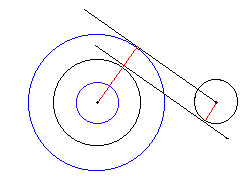Of course there is a case when the solution does not exist.

(Elsewhere there is an interactive illustration to the above construction.)

References

V. Gutenmacher, N. Vasilyev, Lines and Curves: A Practical Geometry Handbook , Birkhauser; 1 edition (July 23, 2004)

40601346