3 Isosceles Trapezoids
What Is It About?
A Mathematical Droodle

Let there be 6 points O₁, O₂, O₃, O₄, O₅ and O₆. Assume also that in the hexagon O₁O₂O₃O₄O₅O₆ there are three pairs of parallel sides: O₁O₂ || O₄O₅, O₂O₃ || O₅O₆ and O₃O₄ || O₆O₁ and that each pair of parallel sides defines an isosceles trapezoid. The vertices of each of the trapezoids lie on a circle. What the applet is supposed to suggest is that if two of the circles coincide, then the third circle coincides with the other two.

(Due to this statement, it is impossible to have all three trapezoids isosceles unless all three circles coincide. The applet, therefore, insures that the red and the blue quadrilaterals are isosceles trapezoids. The green quadrilateral acquires that symmetry if and only if the three circles coincide.)

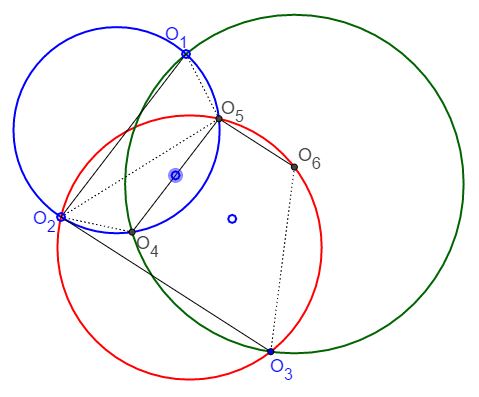
Lemma

Let each side of the hexagon O₁O₂O₃O₄O₅O₆ be parallel to its opposite mate. Then the hexagon is inscribable in a circle if and only if the three pairs of opposite sides define isosceles trapezoids.

Proof ⁽¹⁾

First, assume that the three quadrilaterals O₁O₂O₄O₅, O₂O₃O₅O₆ and O₃O₄O₆O₁ are all isosceles trapezoids. The circumcenter of the first lies on the common perpendicular bisector of O₁O₂ and O₄O₅. The circumcenter of O₂O₃O₅O₆ lies on the common perpendicular bisector of O₂O₃ and O₅O₆. Consider the point S of intersection of the two lines. I wish to show that all six points are equidistant from S.

By construction, points O₁ and O₂ certainly are (from the first trapezoid) as are points O₂ and O₃ (from the second trapezoid). Also by construction, SO₄ = SO₅ and also SO₅ = SO₆.

In the third trapezoid, O₃O₄O₆O₁, we therefore have

SO₁ = SO₃ and SO₄ = SO₆

so that the perpendicular bisectors of the sides O₁O₃ and O₄O₆ cross at S, and, because of the symmetry of the isosceles trapezoid O₃O₄O₆O₁, the common perpendicular bisector of its bases, O₃O₄ and O₆O₁, also passes through S.

This completes the "if" portion of the proof. The "only if" portion is obvious. If a hexagon inscribed in a circle has the sides parallel to their opposites, then the opposite sides do of course define isosceles trapezoids.

Proof ⁽²⁾

The sides of an isosceles trapezoid are equal and so are its diagonals. Any two of the three trapezoids at hand share a diagonal, such that in all there are just three segments: O₁O₄, O₂O₅, and O₃O₆. Any two of the segments serve as diagonals of one of the three trapezoids and are, therefore, equal. Which implies that all three are equal. Having established that, we are now in a position to apply Problem 109 from [Shklyarsky]:

Prove that, if in a hexagon the opposite sides are parallel and the three diagonals joining the opposite vertices are equal, then the hexagon is inscribable in a circle.

A trapezoid with equal diagonals is necessarily isosceles. The common perpendicular bisector of O₁O₂ and O₄O₅ serves as the axis of symmetry of the trapezoid O₁O₂O₄O₅. It passes through the point of intersection of the diagonals O₁O₄ (or their extensions) and O₂O₅ and bisects the angle formed by the two. Similar conclusions could be drawn regarding the other two trapezoids. The three diagonals form a triangle in which the axes of symmetry of the three trapezoids bisect internal angles. The axes of symmetry are concurrent at the incenter of the triangle formed by the three diagonals. Naturally, all six points O₁, ..., O₆ are equidistant from that point.

References

1. Floor van Lamoen, Private communication, May 2002.
2. D. O. Shklyarsky, N. N. Chentsov, I. M. Yaglom, Selected Problems and Theorems of Elementary Mathematics, v 2, Moscow, 1952

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny