Parallel Lines in a Quadrilateral: What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
The applet is intended to suggest the following proposition [Gardiner, Bradley, p. 67]:
| ABCD is a quadrilateral. The line through A parallel to CD meets BD at E and the line through D parallel to AB meets AC at F. Prove that EF is parallel to BC. |
| Buy this applet What if applet does not run? |
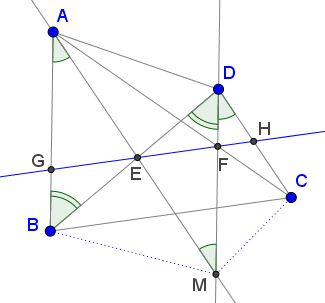
Solution
If AB||CD there is nothing to prove since, in this case, E coincides with B and F with C. Otherwise, let M be the intersection of AE and DF and G, H the intersections of EF with AB and CD, respectively. First consider the trapezoid AMCD.
ΔDFH is similar to ΔMFE, so that
| (1) | DH/FH = EM/EF, or DH/EM = FH/EF. |
Triangles AEF and CHF are also similar, implying
| (2) | CH/AE = FH/EF. |
Together, (1) and (2) give
| (3) | DH/EM = FH/EF = CH/AE, or DH/CH = EM/AE. |
In trapezoid ABMD, triangles ABE and MDE are similar. Therefore we have the ratio
| (4) | EM/AE = DE/BE. |
Together, (3) and (4) imply
| DH/CH = DE/BE. |
Two transversals GH and BC induce equal ratios on sides BD and CD of angle BDC. The transversals are parallel.
Michel Cabart came up with a shorter variant of the proof.
Let I be the intersection of BD and AC. Let g be the homothety with center I mapping BA onto DF, h the homothety with center I mapping DC into EA. Let f the homothety product
We have
| f(B) | = hg(B) | = h(D) | = E and also | |
| f(C) | = gh(C) | = g(A) | = F |
implying f(BC) = EF so that EF is parallel to BC.
Michel has also observed that by a repeated application of one of Thales theorems (the one that claims proportions on parallel transversals which we already used several times above) it is a simple matter to present the same proof while omitting all mention of homotheties:
| IE / IB | = (IE / ID) × (ID / IB) | |
| = (IA / IC) × (IF / IA) | ||
| = IF / IC, |
with the same conclusion as before.
Michel's third message read: "My last remark about this problem. The plain reason why this figure looks so familiar is that it is nothing else than Pappus configuration." You may want to ponder this one before reading further. Just brilliant.
Let ab, cd, and bc be the points at infinity defined by the directions of AB, CD, and BC, respectively. Instead of the quadrilateral ABCD, consider the hexagon BAabCDcd. E is then the intersection of Acd and CD, while F is the intersection of AC and Dab. Let K be the intersection of the third (Pappus) pair, viz., BC and (ab)(cd). By Pappus' theorem, the three points E, F, K are collinear. But K belongs to the line at infinity (ab)(cd), implying that EF is indeed parallel to BC.
References
- A. D. Gardiner, C. J. Bradley, Plane Euclidean Geometry: Theory and Problems, UKMT, 2005
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49551991 |
