Two Circles In a Square II

The applet illustrates the following problem [Tao, pp. 66-68]:

Let $ABCD$ be a square, and let $\kappa$ be the circle with center $B$ passing through $A,$ and let $\ell$ be the semicircle inside the square with diameter $AB.$ Let $E$ be a point on $\ell$ and let the extension of $BE$ meet the circle $\kappa$ at $F.$

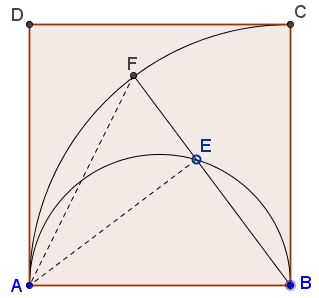
two circles in square - problem

Prove that $\angle DAF = \angle EAF.$

Solution

References

T. Tao, Solving Mathematical Problems, Oxford University Press

two circles in square - problem

Prove that $\angle DAF = \angle EAF.$

Introduce $G$ - the intersection of $AF$ and $\ell$.

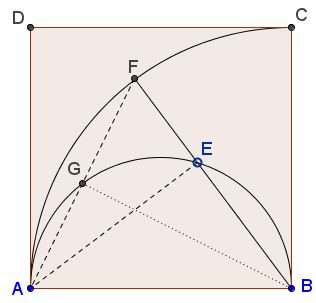
two circles in square - solution

Observe that $AD$ is tangent to both the circles at $A.$ From here, in circle $\kappa$, the angle $DAF$ between the tangent $AD$ and chord $AF$ is half the central angle $ABF:$

$2\angle DAF = \angle ABF.$

In circle $\ell$, for a similar reason, the angle $DAG$ $(= \angle DAF)$ equals the inscribed angle $ABG:$

$\angle DAG = \angle ABG.$

It follows that $\angle ABG$ is half $\angle ABF$ $(= \angle ABE).$ And so is the remaining angle:

$\angle GBE = \angle ABG.$

On the other hand,

$\angle GBE = \angle GAE,$

as inscribed angles subtended by the same arc, which implies the required identity:

$\angle DAF = \angle EAF.$

72109912