Eight Equal Tangents

Tangents from a point to a circle are equal. Tangents to two circles from a point on their radical axis are also equal. The four common tangents to two circles (when all four are available) supply a slew of equal segments. An applet below provides an illustration for a less known fact: the emphasized segments - all eight of them - are indeed equal.

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Let show, for example, that in the diagram below, EK = FL:

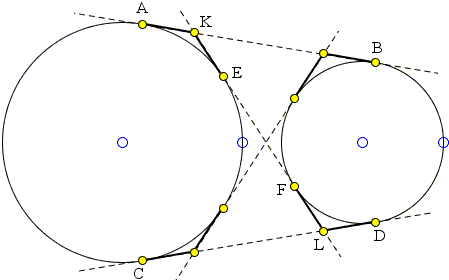
AB = AK + BK   = EK + FK   = EK + (EK + EF)   = 2·EK + EF.

Similarly,

CD = CL + DL   = EL + FL   = (FL + EF) + FL   = 2·FL + EF.

Since AB = CD we also have

2·EK + EF = 2·FL + EF

and, finally, EK = FL.

We could similarly show that in the diagram below also EK = FL.

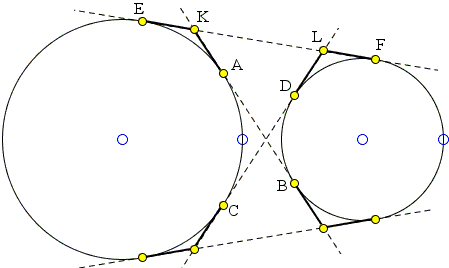
However, the derivation above also works in this case provided some of the segments are allowed to be negative.

References

1. R. Honsberger, More Mathematical Morsels, MAA, 1991, pp. 4-5.

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|