A Multiplicative Identity of Areas in a Triangle

Draw, through point R in the interior of ΔABC, lines JQ, KM, and NP parallel to sides BC, AB, and AC, respectively. Let (Γ) denotes the area of shape Γ. Then

(JMR)(PQR)(KNR) = (JNR)(KQR)(MPR).

Proof

Draw, through point R in the interior of ΔABC, lines JQ, KM, and NP parallel to sides BC, AB, and AC, respectively. Let (Γ) denotes the area of shape Γ. Then

(JMR)(PQR)(KNR) = (JNR)(KQR)(MPR).

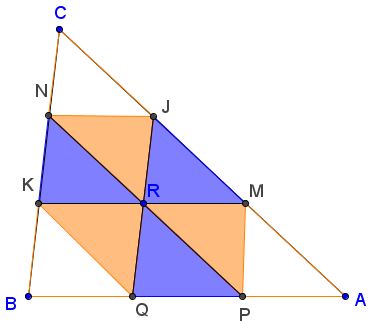
Three parallels through a point in a triangle

Proof

Observe that quadrilaterals JMPQ, KMJN, and KNPQ supply the premises for the corollary of Bui Quang Tuan's lemma. Thus we may conclude that

(MPR)² = (JMR)(PQR),
(JNR)² = (JMR)(KNR).
(KQR)² = (PQR)(KNR).

Multiply all three:

(MPR)²(JNR)²(KQR)² = (JMR)²(PQR)²(KNR)².

Since all the areas involved are positive, taking square root we obtain the required identity:

(JMR)(PQR)(KNR) = (JNR)(KQR)(MPR).

At the site of Vanni Gorni the problem is solved a little differently. It appears that it was first published in 1838 in the Belgian magazine Correspondance Mathématique et Physique edited by A. Quetelet (1796-1874). The same issue was expanded in 1859 in the French Nouvelles Annales de Mathématiques edited by Gerono Terquem.

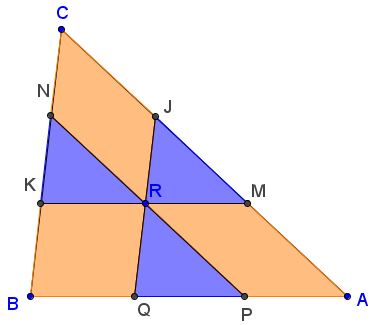
Three parallels through a point in a triangle

Consider ΔCKM. For definiteness sake, assume MR/KM = λ. Then KR/KM = 1 - λ. (JMR)/(CMK) = λ² while (KNR)/(CMK) = (1 - λ)². From here,

(CJRN)/(CMK) = 1 - λ² - (1 - λ)² = 2λ(1 - λ),

implying (CJRN)/(CMK) = 2·√(JMR)/(CMK) · √(KNR)/(CMK), or

(CJRN)² = 4(JMR)(KNR).

Similarly, in triangles AJK and BNP,

(AMRP)² = 4(PQR)(JMR), and
(BKRQ)² = 4(KNR)(PQR).

Multiplying all three and taking the square root, we obtain

(AMRP)(BKRQ)(CJRN) = 8(JMR)(PQR)(KNR)

- the same identity as before but now in terms of parallelograms.

Acknowledgement: I am grateful to a former correspondent for bringing Vanni Gorni's site to my attention.

71866625