Knots on a Torus

The applet below displays the curves that wind on the surface of a torus a prescribed number of times. The applet makes use of the JavaView library and is a slight modification (hopefully, an improvement) of one of their tutorial samples.

Torus is a two dimensional surface defined in a 3d space, which means that, to describe a torus, one needs three coordinates, say (x, y, z), which depend on two parameters. Analytically,

x(u, v) = (R + r cos v) cos u,
y(u, v) = (R + r cos v) sin u,
z(u, v) = r sin v.

Torus is described by a circle of radius r centered at the points of circle x² + y² = R² and located in the plane through the z-axis (or by a rotation of the latter.) Parameter u is responsible for the position of the variable circle relative to the xy-coordinate plane; parameter v describes the position of a point on that circle. Both parameters range over the interval [0, 2π].

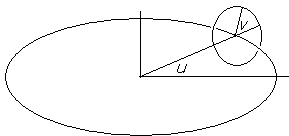
The curves that the applet displays are defined with a single parameter,

u(t) = Ut, v(t) = Zt, t ∈[0, 2π].

Parameter U tells us how many times the curve winds around z-axis. Parameter Z gives the number of turns around the basic circle, x² + y² = R².

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

41143755