What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet may suggest the following assertion: The area of a regular dodecagon (a 12-gon) inscribed into a unit circle is 3. How so?

You can observe in the applet that dodecagon is tiled by 24 isosceles 15°-15°-150° triangles and 12 regular triangles. Two isosceles triangles sharing the base combine into a rhombus with the side equal to that of regular triangles.

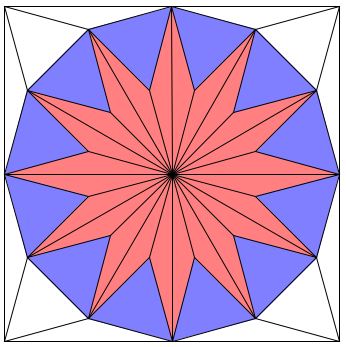
If we look at the square circumscribing the unit circle, we'll count 8 additional isosceles and and 4 regular triangles. Which makes it pretty obvious that the dodecagon takes up 3/4 of the area of the square. But the latter has side 2 and, hence, the area of 4. This gives us 4×3/4 = 3, as desired.

The applet shows how the triangles in the dodecagon's tiling can be rearranged to fill three quarters of the square.

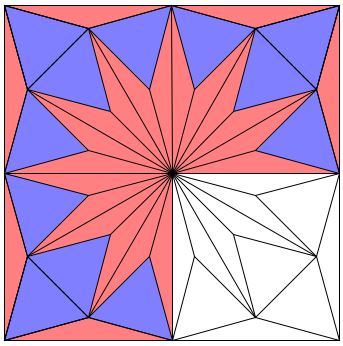
The tiling of the square presented by the applet is known as Kürschak's tile and the theorem about the area of the dodecagon as Kürschak's theorem.

To see that the regular and the 15°-15°-150° triangles indeed tile both the square and the dodecagon it is easier to start with the triangles. Obviously, 24 isosceles triangles compose a 12-pronged star. Let G, M, N be a triple of successive pointed ends and K and L the concave vertices lying between G and M and M and N, respectively. Let O be the center of the star.

∠GKM	= 360° - ∠OKG - ∠OKM
	= 360° - 150° - 150°
	= 60°.

On the other hand, KG = KM by construction. Hence ΔGKM is regular.

The same holds for ΔMLN and the other blue triangles. All are regular and have equal sides. This shows the 12-outisde vertices of the star form a regular dodecagon.

Now we extend the tiling with 8 thin isosceles and 4 regular triangles. Then, say, adding up the angles we see that CGD is a straight line and the same holds for the other three pairs of triangle bases. The four lines form a square because they are parallel to the perpendicular lines EG and FH. Since CG = OF and CF = OG, the C-vertices of the two isosceles triangles CMG and CFN indeed coincide, so that the triangles meet at the corners of the square.

Denote the vertices of the square A, B, C, and D. What remains to be shown that the triangles at the corners of the square with the base on the sides of the dodecagon are regular.

They are certainly isosceles. For example, by symmetry, CM = CN. Also ∠MCN = 90° - 15° - 15°, so that ∠MCN = 60°. And we are finished.

The theorem is named after the Hungarian mathematician Jozsef Kürschak (1864-1933) famous for the Kürschak Competition, the stepping stone of many Hungarian mathematicians.

Alexanderson and Seydel discussed Kürschak's tile alongside a problem from the 1977 International Mathematical Olympiad (I thank Douglas Rogers for bringing the paper by Alexanderson and Seydel to my attention.) The problem is illustrated by the following diagram:

Equlateral triangles are constructed on the sides of a square inwardly. Their apexes form a square. Prove that the midpoints of the sides of the latter and the intersections of the side lines of the triangles form a dodecagon.

(It goes without saying that the apexes of the equilateral triangles constructed outwardly on the sides of the inner square coincide with the vertices of the original one.)

As a final remark, observe that the area of a unit circle (which is π) is greater that the area of the inscribed dodecagon (which, as we saw, is 3.) As a consequence, we obtain the inequality π > 3.

References

1. G. L. Alexanderson, K. Seydel, Kürschak's tile, Math. Gaz. 62 (421) (1978), 192-196
2. D. Wells, Curious and Interesting Geometry, Penguin Books, 1991

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny