Parallel Lines in a Triangle
The following problem has been suggested by Vladimir Nikolin (June 17, 2012):
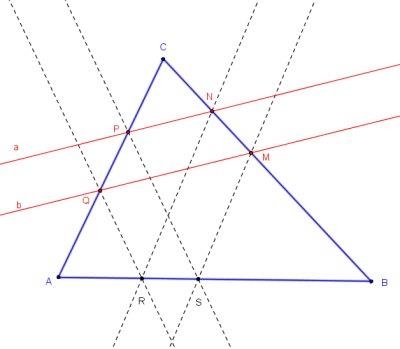
Given is ΔABC. Let a||b and a∩AC = P, a∩BC=N, b∩AC = Q, b∩BC = M. Construct (ruler-compass) points R, S on AB so that QR||PS and NR||MS.
|Mail| |Fron page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Given is ΔABC. Let a||b and a∩AC = P, a∩BC=N, b∩AC = Q, b∩BC = M. Construct (ruler-compass) points R, S on AB so that QR||PS and NR||MS.

Soluiton 1
The solution below is by Hubert Shutrick who signed it up with "Facile comme bonjour!" (French for "Easy as pie!") The Geogebra applet illustrates his solution (points A, B, C, P, Q, N are draggable):
Let Q' and A' be on the ray MP such that MQ' = PQ and MA' = PA, let the line through A' parallel with Q'N meet BC at A''. Then, the lines through N and M parallel with A''A meets AB at R and S respectively.
Solution 2
Vladimir Nikolin supplied the following solution.

Analysis: Let X, Y, Z denote the midpoints of segments MN, PQ, and RS, respectively. From Thales' theorem
AY/AZ = PQ/RS, BZ/BX = RS/MN and CX/CY = MN/PQ.
If we multiply these, we get (AY/AZ) × (BZ/BX) × (CX/CY) = 1, or
(AY/CY) × (CX/BX) × (BZ/AZ) = 1.
It means (the converse of Ceva's theorem) that triangles ABC and XYZ are perspective in a point. In addition, YZ||PS||QS (PQRS is a trapezoid, YZ is its midline).
Construction: Let AX and BY intersects in O, CO and AB intersects in Z. Draw two parallels to YZ from P and Q.
Solution 3
Hubert has come up with a simplified version of his solution: let N' be the point on AM such that QN'||PM, then NN' meets AB at R. I placed his generalization on a separate page.
|Mail| |Fron page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
