Seven Concyclic Points
The problem below was posted posted at the CutTheKnotMath facebook page by Cõ Gẫng Lên:
Points \(N, P, Q\) are collinear. For a fourth point \(M,\) consider circumcircles, \((A)\) of \(\Delta MNP\), \((B)\) of \(\Delta MPQ\), \((C)\) of \(\Delta NPQ.\) In addition, let \(A_{1}\) be the intersection of \(CN\) and \(BP,\) \(B_{1}\) the intersection of \(AP\) and \(CQ,\) and \(C_{1}\) the intersection of \(AN\) and \(BQ.\)
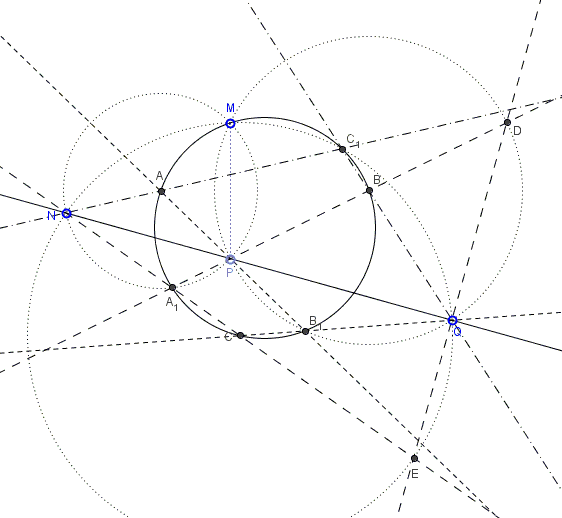
Prove that points \(M, A, B, C, A_{1}, B_{1}, C_{1}\) are concyclic.
(The applet below illustrates the problem.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Points \(N, P, Q\) are collinear. For a fourth point \(M,\) consider circumcircles, \((A)\) of \(\Delta MNP\), \((B)\) of \(\Delta MPQ\), \((C)\) of \(\Delta NPQ.\) In addition, let \(A_{1}\) be the intersection of \(CN\) and \(BP,\) \(B_{1}\) the intersection of \(AP\) and \(CQ,\) and \(C_{1}\) the intersection of \(AN\) and \(BQ.\)

Prove that points \(M, A, B, C, A_{1}, B_{1}, C_{1}\) are concyclic.
Solution
We already proved that points \(M,A,B,C\) are concyclic. This followed from the identity \(\angle AMB+\angle ACB=180^{\circ}\) which was a consequence of the fact that triangles \(AMN\) and \(BMQ\) are obtained from each other by a rotation around \(M\) with subsequent homothety with \(M\) as center. The combined transformation maps line \(AN\) onto \(BQ\) so that \(\angle AC_{1}B\) is exactly the angle of rotation, implying \(\angle AC_{1}B=\angle AMB\) which places \(C_1\) on the circumcircle \(MABC.\)
... to be continued ...
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73583125
