Three Collinear and Four Concyclic Points

The problem below is a part of a question posted at the CutTheKnotMath facebook page by Cõ Gẫng Lên:

Points \(N, P, Q\) are collinear. For a fourth point \(M,\) consider circumcircles, \((A)\) of \(\Delta MNP\), \((B)\) of \(\Delta MPQ\), \((C)\) of \(\Delta NPQ.\)

When three points are collinear some four points are concyclic - problem

Prove that points \(M, A, B, C\) are concyclic.

(The applet below illustrates the problem.)

Solution

Points \(N, P, Q\) are collinear. For a fourth point \(M,\) consider circumcircles, \((A)\) of \(\Delta MNP\), \((B)\) of \(\Delta MPQ\), \((C)\) of \(\Delta NPQ.\)

When three points are collinear some four points are concyclic - problem

Prove that points \(M, A, B, C\) are concyclic.

Solution

For definiteness sake, let point \(P\) lie between \(N\) and \(Q\). Angles \(NPM\) and \(MPQ\) are supplementary: \(\angle NPM=180^{\circ}-\angle MPQ.\) \(\angle NPM\) is inscribed in circle \((A)\) so that central angle \(NAM\) is twice as large. In circle \((B)\), \(\angle MBQ=2(180^{\circ}-\angle MPQ)=\angle NAM.\) It follows that two isosceles triangles \(AMN\) and \(BMQ\) are similar. In addition, one can be obtained from the other by a rotation around \(M\) followed, if necessary, by a homothety with center \(M\).

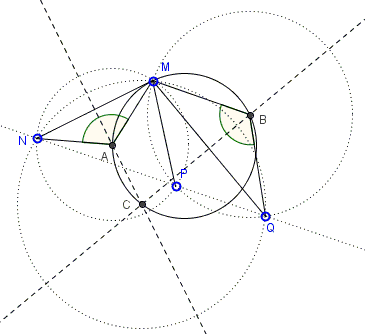
When three points are collinear some four points are concyclic - solution

Under the two trasformations the perpensicular bisector of \(MN\) maps onto the perpendicular bisector of \(MQ.\) Let \(C'\) be the point of intersection of the two bisectors: \(C'N=C'M=C'Q,\) implying \(C'=C.\) Also, since \(C\) is defined by a rotation around \(M\), and \(MA\) is mapped onto \(MB,\) \(\angle AMB+\angle ACB=180^{\circ},\) making the four points \(M,A,B,C\) concyclic.

In a little different guise and with a different proof the problem appears elsewhere

71948699