A Property of Right Isosceles Triangle

A property of right isosceles triangles has been observed by Emmanuel Antonio José García who posted a statement at the CutTheKnotMath facebook page. What is it? The applet below may give you an idea.

A few words

Emmanuel Antonio José García has observed that

For any point $E$ on the hypotenuse $AB$ of a right isosceles triangle $ABC$, the circumradii of triangles $ACE$ and $BCE$ are equal.

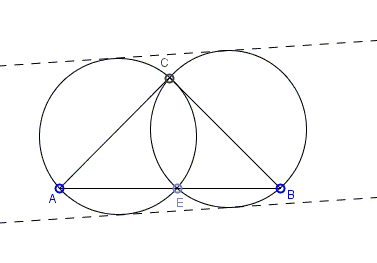
two circumcircles in right isosceles triangle

This follows from the Law of Sines. The circumradius of $\Delta ACE$ is equal to $\displaystyle\frac{2AC}{\mbox{sin}(AEC)},$ while that of $\Delta BCE$ is equal to $\displaystyle\frac{2BC}{\mbox{sin}(BEC)}.$ Now, since $AC=BC$ and angles $AEC$ and $BEC$ are supplementary such that $\mbox{sin}(AEC)=\mbox{sin}(BEC),$ we that the two radii are indeed equal.

Note: As Hubert Shutrick observed, the statement is true because the two circles share chord $CD$ and the inscribed angles subtended by $CD$ in the two circles are equal. Thus the statement holds for any isosceles triangle and a point on its base.

71537306