PPC: Apollonius' Problem with Two Points and a Circle<
Below I give an Euclidean construction to a variant of the Problem of Apollonius:
Find a circle through two given points \(C\) and \(D \) and tangent to a given circle \(A(B),\) with center at \(A\) and passing through \(B\):
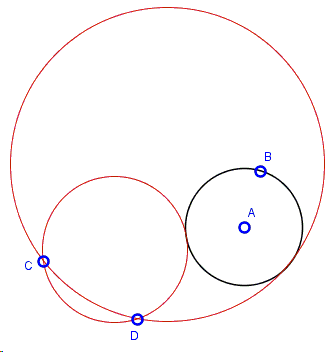
Rather obviously the problem has no solutions if the given circle separates the given points (i.e., if one of the points is inside, the other outside the circle.)
(The applet below illustrates the proof. Points \(A, B,C,D,E\) are draggable. This permits changing the configuration, but within certain limitations.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle through two given points \(C\) and \(L \)and tangent to a given circle \(A(B),\) with center at \(A\) and passing through \(B\):

Start with finding any circle that passes through the given points and intersects with the given circle in two point, say, \(F\) and \(G\):
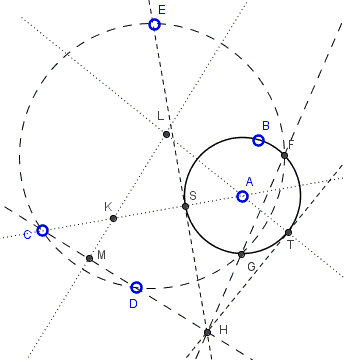
Let \(H\) be the intersection of \(CD\) and \(FG\). Find \(HS\) and \(HT\) - the tangents from \(H\) to \(A(B).\) Find the intersections \(K\) and \(L\) of the perpendicular bisector of \(CD\) with \(AS\) and \(AT,\) respectively. Circles \(K(S)\) and \(L(T)\) solve the problem.
Why does the construction work?
Assuming the problem solved, let \((O)\) denote the auxiliary circle. Then \(FG\) is the radical axis of \((O)\) and \(A(B)\), the common tangent at \(S\) is the radical axis of \(K(S)\) and \(A(B),\) while the tangent at \(T\) is the radical axis of \(L(T)\) and \(A(B).\) Lastly, \(CD\) is the radical axis of any pair of (O), \(K(S)\), or \(L(T)\). It follows that \(H\) is the radical center of the three circles \(K(S),\) \(A(B),\) and \((O)\), as well as the radical center of \(L(T),\) \(C(A, B),\) and \((O)\). You can notice by dragging point \(E\) on the circle \((O)\) in the applet that \(H\) does not depend on the position of \((O).\) Thus \(H\) is uniquely determined as the intersection of \(FG\) and \(CD\).
The problem has two solutions.
References
- N. Altshiller-Court, College Geometry, Dover, 1980, #470
- J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971, p. 168
- R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 2007, #169
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579122
