LLC: Apollonius' Problem with Two Lines and a Circle
Below I give an elementary Euclidean construction to a variant of the Problem of Apollonius:
Find a circle tangent to two given lines \(m_1\) and \(m_2\) and a given circle \((O)\):
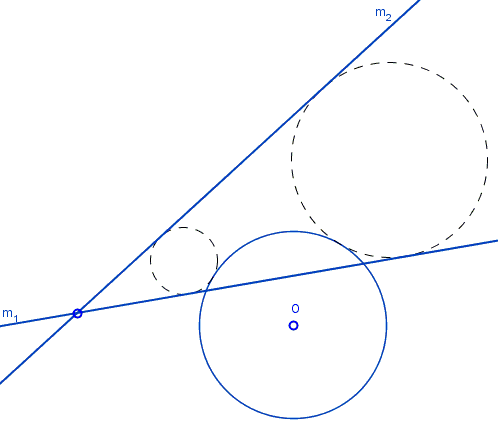
Rather obviously the problem has no solutions if the given line separates the given points (i.e., if the points are on different sides of the line.)
(The applet below illustrates the construction.)
Created with GeoGebra
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle tangent to two given lines \(m_1\) and \(m_2\) and a given circle \((O)\):

The center of a circle that solves the problem lies on the bisector of an angle formed by the two given lines. (If the lines are parallel, the same role is played by the line midway between the two.) The circle, therefore, is symmetric in the bisector. Let \((O')\) be the reflection in the bisector of the given circle \((O).\)
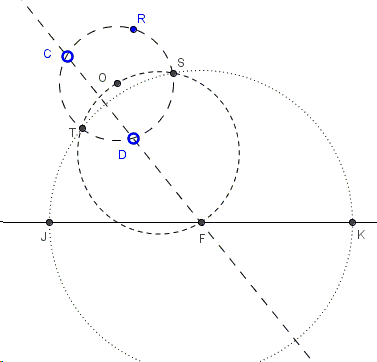
If we increase the radius of the solution by the radius of \((O)\), the resulting circle will pass through two points, \(O\) and \(O'.\) Incidentally, it will also be tangent to a line parallel to, say, \(m_1\) and at the distance from the latter equal to the radius of \((O).\)
This suggests a construction: First find the reflection \(O'\) of \(O\) in the bisectors of an angle formed by the two given line. Then shift one of the line to the distance equal to the radius of \((O).\) Finally, solve the resulting PPL problem.
References
- N. Altshiller-Court, College Geometry, Dover, 1980, #514
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73576728
