PPL: Apollonius' Problem with Two Points and a Line
Below I give an Euclidean construction to a variant of the Problem of Apollonius:
Find a circle through two given points \(C\) and \(D \) and tangent to a given line \(AB\):
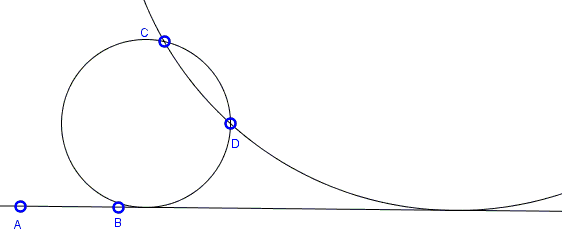
Rather obviously the problem has no solutions if the given linle separates the given points (i.e., if the points are on different sides of the line.)
(The applet below illustrates the proof. Points \(A, B,C,D,R\) are draggable. This permits changing the configuration, but within certain limitations.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle through two given points \(C\) and \(D \) and tangent to a given line \(AB\):

The solution is a pure application of the Power of a Point Theorem. Start with finding any circle \(O(CDR)\) that passes through given points:
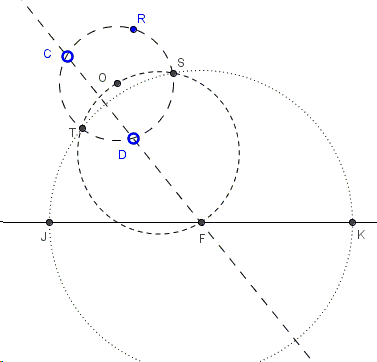
Let \(F\) be the intersection of \(CD\) and \(AB\). If \(J\) is a point where a sought cricle through \(C\) and \(D\) touches line \(AB\), then, by the Power of a Point Theorem, \(CF\cdot DF=FJ^2.\) For the same reason, if, say, \(FS\) is tangent to \(O(CDR)\) at \(S\) then also \(CF\cdot DF=FS^2.\) Now, to obtain \(S\) we only need to draw a circle on \(FO\) as a diameter. This intersects \(O(CDR)\) in \(S\) and another point \(T\). The circle \(F(S)\) with center \(F\) through \(S\) intersects \(AB\) in two points \(J\) and \(K\). The circumcircles \((CDJ)\) and \((CDK)\) solve the problem.
Sometimes the problem is formulated a little differently. Note that the two given points define a pencil of (coaxal) circles. Any pair of the circles from the pencil has \(CD\) as the radical axis; and the perpendicular bisector of \(AB\) houses the centers of all the circles in the pencil. So, the problem is equivalent two finding a circle in the given pencil tangent to a given line.
References
- N. Altshiller-Court, College Geometry, Dover, 1980, #452
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73593163
