Orthic Semiperimeter
There are many many formulas for the area of a triangle. Among the most useful is \(S = pr\), where \(S\) is the area, \(p\) the semiperimeter, and \(r\) the inradius of a triangle. Among the little known is the one Ross Honsberger discovered in the end of the 19th century publication Mathematical Visitor:
\(S = qR\),
where, as before, \(S\) is the area of a triangle, \(R\) its circumradius, and \(q\) the semiperimeter of its orthic triangle.
The insight into this formula comes from Fejér's solutions to the Fagnano's problem.
Proof
Let \(AD\), \(BE\), and \(CF\) be the altitudes in \(\Delta ABC\). Triangle \(DEF\) is known as the orthic triangle of \(\Delta ABC\). Let \(E'\) and \(E''\) be the reflections of \(E\) in \(BC\) and \(AB\), respectively. Due to the mirror property of the altitudes, \(E'DFE''\) is a straight line and \(\Delta E'BE''\) is isosceles \((BE' = BE = BE'')\). Also, by the construction, \(\angle E'BE'' = 2\angle ABC\).
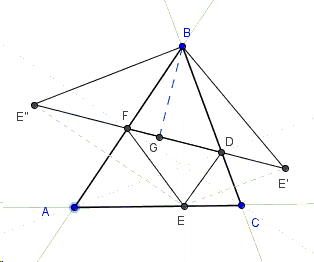
Most importantly,
\( \begin{align} E'E'' &= E'D + DF + FE'' \\ &= DE + DF + EF \\ &= 2q. \end{align} \)
It thus follows that, for \(G\) being the foot of the altitude from \(B\) in \(\Delta E'BE''\), \(q = E'G = BE'\cdot\mbox{sin}\angle ABC = BE\cdot\mbox{sin}\angle ABC\). So \(q = BE\cdot\mbox{sin}\angle ABC\), but, by the Law of Sines, \(\displaystyle 2R = \frac{AC}{\mbox{sin}\angle ABC}\). Also, as is well known, \(\displaystyle S = \frac{AC\cdot BE}{2}\). Now, combining the three identities gives the required result:
\( \begin{align} q &= BE\cdot\mbox{sin}\angle ABC \\ &= \frac{2S}{AC}\cdot \frac{AC}{2R} \\ &= \frac{S}{R}. \end{align} \)
References
- R. Honsberger, Mathematical Diamonds, MAA, 2003, p 19
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581811
