Three Common Chords in Three Concurrent Circles
When two circles intersect, the common chord through one of the intersections is the longest when its endpoints are diametrically opposite the other point of intersection in the two circles. This property is extended to three concurrent circles.
Circles \((A)\), \((B)\), and \((C)\) concur at point \(D\). Chords \(KL,\) \(LM\), and \(KM\) pass through the other points of intersection \(G,H,F\)
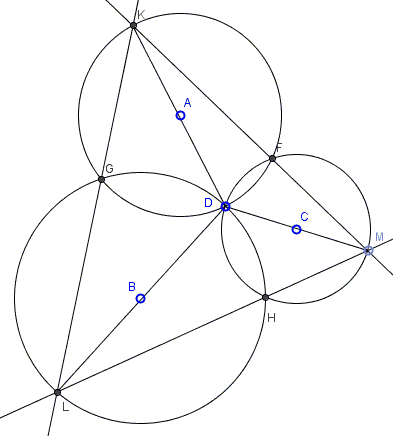
Prove that, if one of the segments \(DK\), \(DL\), \(DM\) is a diameter in the respective circle, so are the other two.
(The applet below illustrates the problem.)
This is a return to a configuration that we met several times in the past. The statement will actually work for any number of concurrent circles.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580780
