A Characterization of the Euler LineThe applet below illustrates a view point on problem 1814 from the Mathematics Magazine. The problem has been proposed by Michael Goldenberg and Mark Kaplan, The Ingenuity Project, Baltimore Polytechnic Institute, Baltimore, MD. A solution by Herb Beiley, Rose Hulman Institute of Technology, Terre Haute, IN, has been published in Vol 83 (2010), No 1, pp 68-69.
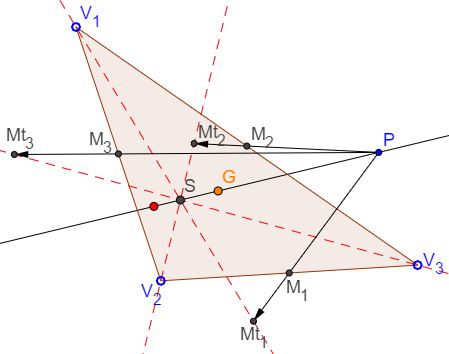
Let V1V2V3 be a triangle with circumcenter O, and let M1, M2, M3 be the midpoints of V2V3, V1V3, and V1V2, respectively. For
I do not remember being so disappointed on reading a problem or a solution in the Mathematics Magazine. Compared to the American Mathematical Monthly (both published by the Mathematical Association of America), the Mathematics Magazine is intended to a broader audience that may include high school math teachers or even students. But then its editors have probably even greater responsibility to avoid publishing tasteless exercise disguised as a piece of mathematics. My contention is that the problem's setup has actually very little to do with the Euler line. A little generalization shows that this is indeed so:
Let P be a point in the plane of ΔV1V2V3, and let M1, M2, M3 be the midpoints of V2V3, V1V3, and V1V2, respectively. For
Observe that for P = O, the circumcenter of V1V2V3, the latter formulation reduces to that of the original problem because the Euler line passes through both G and O. (The applet actually illustrates the generalization.)
The published solution replaces the problem with the following one:
Let P be a point on the perpendicular bisector of side V1V2 and let Mtk be the point defined by PMtk = tPMk. Then lines VkMtk, k = 1, 2, 3, are concurrent, and that the locus of all such points of concurrence is a line. The line is the Euler Line if and only if P is chosen to be the circumcenter.
I loath to reproduce the whole proof. The idea is to choose the coordinate system with O at the center and the base of the triangle symmetric in the y-axis. Such selection simplifies the analytic algebra that follows. Now observe that both formulations are somewhat loose in defining Mtk. The confusion here is between affine (consisting of points) and vector spaces. By itself, say, OMtk = tOMk define a vector, not a point. The intention is apparently to the point So let's proof the following statement:
Let P be a point in the plane of ΔV1V2V3, and let M1, M2, M3 be the midpoints of V2V3, V1V3, and V1V2, respectively. For
Note that, for a fixed t, function Ft(M) = P + t(M - P) is a homothety transformation with center P and coefficient t. This homothety maps Mk onto Mtk, k = 1, 2, 3, and the whole ΔM1M2M3 onto ΔMt1Mt2Mt3. Note also, that ΔM1M2M3 is also a homothetic image of ΔV1V2V3. In this case, the homothety, say, F has center G and coefficient -1/2. It follows that ΔMt1Mt2Mt3 is obtained from ΔV1V2V3 by a product (successive application) of two homotheties. Such a product is also a homothety (unless it is a translation) with center on the line joining the centers of the two homotheties, F and Ft, i.e., G and P. (The proof of this result is not difficult. It is well illustrated by the three circles theorem.) Thus for every t, the center of homothety that maps ΔV1V2V3 onto ΔMt1Mt2Mt3 is on line PG. But this homothety maps Vk onto Mtk so that line VkMtk passes through the center of homothety, meaning that this is where the three lines VkMtk, k = 1, 2, 3, concur. PG becomes the Euler line for any P on GO.  |Activities| |Contact| |Front page| |Contents| |Geometry| |Store| Copyright © 1996-2012 Alexander Bogomolny |
| 41143729 |
