Euclid I.43 Extended: What Is This About?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyThe applet illustrates an extension of Euclid I.43 that is essentially due to Quang Tuan Bui.
| What if applet does not run? |
Through point X inside the parallelogram ABCD draw lines MP||BC and NQ||AB. Euclid I.43 asserts that, if X lies on the diagonal BD then the areas of the off-diagonal parallelograms XNCP and AMXQ are equal. The extension concerns the case where X does not lie on the diagonal. There are two ways to handle this situation. In the applet we distinguish between the cases where X is inside ΔABD and where X is inside ΔBCD. The distinction is made purely for convenience. Both extensions could be demonstrated regardless of the location of X.
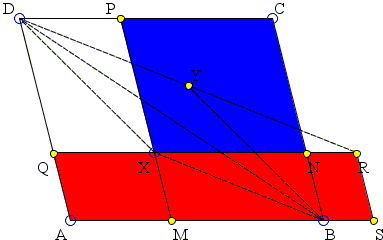
Thus, first assuming that X is inside ΔABD, below the diagonal BD. Then
|
Let XBYD be a parallelogram, DY intersect NQ in R and RS||BC, with S on AB. Then |
It follows that parallelogram MSRX makes up for the difference in areas of XNCP and AMXQ:
|
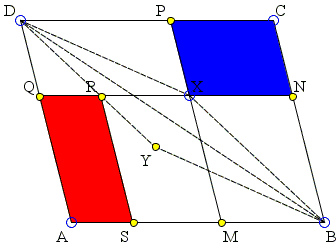
When X is in ΔBCD, the claim is that again Area(ASRQ) = Area(XNCP), with exactly the same construction.
|
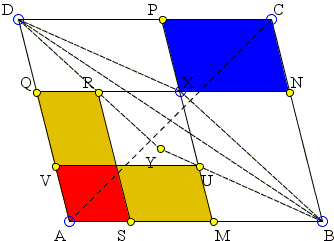
In both case, checking the box "areas on the same side of BD", shows to orange parallelograms. The two also have equal areas. This means (and follows from the fact) that the point of intersection of RS and UV (not shown) lies on the line AX, the diagonal of parallelogram AMXQ. This is just a direct application of Euclid I.43.
|
For a proof (Quang Tuan Bui), let W be the intersection of DR with AB, K is the intersection of RS and CD, E and F the intersections of a line through W parallel to BC with NQ and CD, respectively.
| What if applet does not run? |
Then, since SWER and BWRX are parallelograms,
| ER = BW - NR = RX - NR = NX |
implying that parallelograms REFK and XNCP are congruent. By Euclid I.43 (in parallelogram AWFD),
| Area(ASRQ) = Area(REFK). |
So we get
| Area(ASRQ) = Area(XNCP). |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580143
