|
|
|
|
|
|
|
|
|
Two Quadruplets of Tangent Circles: What is this about?
|
| Buy this applet What if applet does not run? |
Copyright © 1996-2008 Alexander Bogomolny
H. M. S. Coxeter (born February 9, 1907) died on March 31, 2003. In July 2002, he gave a lecture at the János Bolyai Conference on hyperbolic geometry. The lecture was titled "An Absolute Property of Four Mutually Tangent Circles". He began with stating Philip Beecroft's Theorem in Beecroft's own words:
| If any four circles be described to touch each other mutually, another set of four circles of mutual contact may be described whose points of contact shall coincide with those of the first four. |
(Philip Beecroft was an amateur mathematician who also rediscovered Descartes' formula.)
| Buy this applet What if applet does not run? |
After stating the theorem and displaying a transparency, Coxeter added
| The figure makes the theorem almost obvious, but for the sake of completeness it seems desirable to consider further details. |
While I got a description of the event second hand from a recently published Coxeter's biography and did not see either Beecroft's original proof or that of Coxeter's, I agree with him on both counts: the figure makes the theorem almost obvious but further details will not be out of place either.
|
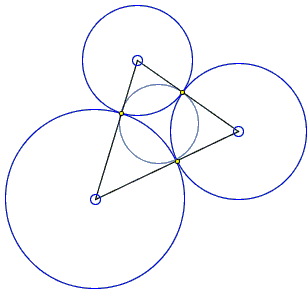
Let there be three mutually tangent circles. (I shall only consider the case of external tangency.) The three common tangents at the points of tangency meet at the radical center of the three circles. The tangents drawn from the radical center to the circles are all of equal length. Also, the lines joining the centers of the circles pass through the points of tangency and are perpendicular to the tangents. They form a triangle. It follows that the radical center of the circles serves as the incenter of the latter. Hence, the incircle passes through the points of tangency and is orthogonal to all three.
Any two circles of the second quadruplet, pass through one of the points of tangency. At this point, they are both orthogonal to the same line (and to the same circles.) Therefore, they are tangent to each other.
The theorem is also easily proved algebraically. Denote the three circles C(A, ra), C(B, rb), C(C, rc), where A, B, C are there centers and ra, rb, rc their radii. Also, introduce three quantities:
| (1) |
a = rb + rc b = rc + ra c = ra + rb. |
Consider the triangle ABC with the side lengths a, b, c. Investigating the lengths of the segments from the vertices to the points of tangency of the incircle with the sides we are led to the system
| (2) |
a = x + y b = y + z c = z + x. |
But this system has a unique solution, so that the points of tangency of the incircle of ΔABC are exactly the points of tangency of the circles C(A, ra), C(B, rb), C(C, rc).
References
- S. Roberts, King of Infinite Space, Walker & Company, 2006
Copyright © 1996-2008 Alexander Bogomolny
| 29284644 |  |
|