Nine Squares: What Is This About?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet presents a configuration of squares with a sole control that allows changing their sizes. However, the small black square does not appear to be partaking of the feast - its size remains constant. How do the other squares change?
To answer this question, denote the side length of the blue square as a, and that of the small red square c. In terms of a and c we are able to express the dimensions of eight squares right away:
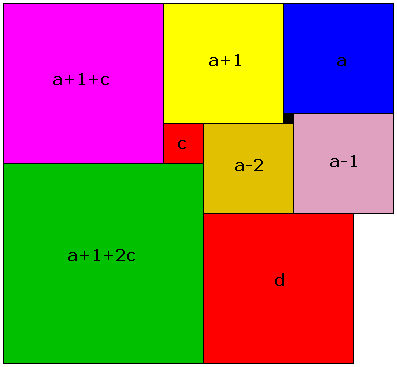
Following the three top squares we find that the horizontal extent of the resulting shape is
a + (a + 1) + (a + 1 + c) = 3a + 2 + c.
On the other hand, starting with the square in the lower left corner and proceeding through the orange and pink squares we find the same quantity equal to
(a + 1 + 2c) + (a - 2) + (a - 1) = 3a - 2 + 2c.
Equating the two we obtain that c = 4, independent of a! When other squares change, the red square in the middle maintains a fixed side of 4! Interestingly this is not the only square with this property. You may notice another red square at the bottom right. It too preserves its size of 15. (You can verify this in a similar manner.)

Now, in addition, the applet helps resolve the following question: is there a rectangle that can be split into unequal squares? The answer is positive and can be observed for

The rectangle then has the dimensions 32×33. These rectangle and its dissection into 9 unequal squares has been discovered in 1925 by Z. Morón. This led to the question of whether a dissection into pairwise unequal squares is possible for a square. The history and some theory of the problem have been discussed by Howard Eves and Martin Gardner: R. Sprague reported a 55 pieces dissection in 1939. In 1940, R. C. Brooks, C. A. B. Smith, A. H. Stone, and W. T. Tutte found a 26-piece dissection. A 24-piece dissection has been published in 1948 by T. H. Willcocks.
It appears that the record has been holding out since then.
References
- H. Eves, A Survey of Geometry, Allyn and Bacon, 1972
- M. Gardner, The Second Scientific American Book of Mathematical Puzzles and Diversions, U. of Chicago Press, 1987
- J. G. McLoughlin et al, Jim Totten's Problems of the Week, World Scientific, 2013, #346
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73567607
