Pythagorean Theorem:
Some False Proofs
Introduction
Even smart people make mistakes. Some mistakes are getting published and thus live for posterity to learn from. I'll list below some fallacious proofs of the Pythagorean theorem that I came across. Some times the errors are subtle and involve circular reasoning or fact misinterpretation. On occasion, a glaring error is committed in logic and leaves one wondering how it could have avoided being noticed by the authors and editors.
Proof 1
One such error appears in the proof X of the collection by B. F. Yanney and J. A. Calderhead (Am Math Monthly, v.3, n. 6/7 (1896), 169-171.)

Suppose the theorem true. Then $AB^{2} = AC^{2} + BC^{2},\;$ $BC^{2} = CD^{2} + BD^{2},\;$ and $AC^{2} = AD^{2} + CD^{2}.\;$ Combining the three we get
$AB^{2} = AD^{2} + 2CD^{2} + BD^{2}.$
But $CD^{2} = AD\cdot BD.\;$ Therefore,
$AB^{2} = AD^{2} + 2AD\cdot BD + BD^{2}.$
From which
$AB = AD + BD,$
which is true. The supposition is true.
Critique
By the same token, assume $1 = 2.\;$ Then, by symmetry, $2 = 1.\;$ By Euclid's Second Common Notion, we may add the the two identities side by side: $3 = 3.\;$ Which is true, but does not make the assumption $1 = 2\;$ even one bit less false.
As we know, falsity implies anything, truth in particular.
Proof 2
This proof is by E. S. Loomis (Am Math Monthly, v. 8, n. 11 (1901), 233.)
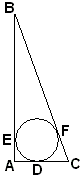
Let $ABC\;$ be a right triangle whose sides are tangent to the circle $(O).\;$ Since $CD = CF,\;$ $BE = BF,\;$ and $AE = AD = r =\;$ radius of circle, it is easily shown that
$(CB = a) + 2r = (AC + AB = b + c).$
And if
(1)
$a + 2r = b + c$
then $(1)^{2} = (2):$
(2)
$a^{2} + 4ra + 4r^{2} = b^{2} + 2bc + c^{2}.$
Now if $4ra + 4r^{2} = 2bc,\;$ then $a^{2} = b^{2} + c^{2}.$ But $4ra + 4r^{2}\;$ is greater than, equal to, or less than $2bc.$
If $4ra + 4r^{2} \gt or \lt 2bc,\;$ then $a^{2} + 4ra + 4r^{2} \gt or \lt b^{2} + 2bc + c^{2};\;$ i.e. $a + 2r \lt\;$ or $\gt b + c,\;$ which is absurd. Hence, $4ra + 4r^{2} = 2bc\;$ and, therefore, $a^{2} = b^{2} + c^{2}.\;$
This proof is accompanied by an Editors' Note:
So far as we know, this proof has not been given before. If it has not been published before, it may be properly called a new proof. Dr. Loomis asks if any one can derive, by this method, a direct proof - the one above being indirect.
Critique
The proof is incorrect, let alone indirect, and generally written in a style that would not be acceptable nowadays. The main problem, however, is the circularity of the argument: the proof uses the Pythagorean identity it set out to establish.
In a subsequent issue of the magazine (Am Math Monthly, v. 8, n. 12 (1901), 258), the editors admit the mishap and quote Prof. B. F. Yanney to the effect that "such reasoning as employed in the proof given by Dr. Loomis would make $4ar = b^{2} + c^{2}\;$ or $4r^{2} = b^{2} + c^{2}\;$, or even $r^{2} = b^{2} + c^{2}.\text{"}\;$
A correct and also direct proof has been supplied by F. L Sawyer. Starting with (1),
(3)
$2a + 2r = a + b + c.$
Such that,
$4ar + 4r^{2} = 2r(a + b + c).$
But evaluating the area of $\Delta ABC\;$ in two different ways (see proof #42)
$r(a + b + c)/2 = bc/2.$
Hence,
(4)
$2r(a + b + c) = 2bc.$
By substituting (1) into (4) we obtain
$4ra + 4r^{2} = 2bc.$
Because of (2) we now get the desired $a^{2} = b^{2} + c^{2}.\;$
Remark
Note that (3) has been known to Liu Hui and on which is based dissection proof #45 by Douglas Rogers. In a private correspondence, Douglas also mentioned that Loomis included Sawyer's proof as the eighty-sixth algebraic proof in his compilation The Pythagorean Proposition without reference to his earlier erroneous effort, but claiming that he hit on it for himself before seeing the issue of The Monthly with Sawyer's proof. He also makes reference to Fourrey.
Proof 3
This proof appears as the geometric proof 22 in Loomis' collection. Loomis refers to a 1914 publication by J. Versluys which listed 96 proofs of the Pythagorean proposition. The proof at hand appears as Fig. 44, p. 43.

Critique
While the proof looks like many other proofs by dissection and rearrangement, this one is not complete in that the construction does not go through where one of the legs of the given triangle is essentially less than the other:

The original diagram does not provide a clue as to the handling of a more general case. (The diagrams above have been obtained with a dynamic illustration.)
Proof 4
This is what could be called a trigonometric proof. Several times it was suggested for the inclusion on the Pythagorean page until Eng. Marìa L. Mean, a retired professor at Havana University, pointed out that's the right place for the derivation is among other false proofs. So here it goes.
In a right-angled $\Delta ABC,$ let $a,\;$ $b\;$ be its legs, $c\;$ its hypotenuse, and $\beta\;$ the angle opposed to leg $\;b$. Then, by the definition of the trigonometric functions
$\displaystyle\begin{align} \sin \beta = \frac{b}{c},\\ \cos \beta = \frac{a}{c}. \end{align}$
As is well known, the sum of $\sin^{2} \beta\;$ and $\cos^{2} \beta\;$ is equal to 1:
$\sin^{2} \beta + \cos^{2} \beta = 1,$
which is a fundamental trigonometric identity. Consequently,$(b/c)^{2} + (a/c)^{2} = 1$
implying $a^{2} + b^{2} = c^{2}.$
Critique
The identity $\sin^{2} \beta + \cos^{2} \beta = 1\;$ is indeed fundamental in trigonometry. However, its derivation is based on the Pythagorean theorem, to start with. Thus, the trigonometric "proof" above may well serve as an example of the circular reasoning, a vicious circle as the latter is sometimes referred to.
A Later Remark
As it comes out $\sin^{2} \beta + \cos^{2} \beta = 1\;$ admits a proof independent of the Pythagorean theorem but based solely on the subtraction formulas for sine and cosine. Thus my critique of the above proof should be taken with the grain of salt. It nonetheless can be used in a polemique. Any one who promotes the above proof with no knowledge as to how to derive $\sin^{2} \beta + \cos^{2} \beta = 1\;$ with no recourse to the Pythagorean theorem makes a severe logical mistake.
Proof 5
A mistake of a higher order is sometimes committed by more advanced students of mathematics who went beyond trigonometry and ventured into the multidimensional geometry. In multidimensional spaces whose elements are vectors, one often defines what is known as the scalar product and then also an angle between two vectors. Say, for two vectors $\overline{a}\;$ and $\overline{b},\;$ if the scalar product is denoted $\overline{a}\cdot \overline{b},\;$ then the angle $\gamma\;$ between the two is defined via the cosine function as in:
$\displaystyle\cos \gamma = \frac{\overline{a}\cdot \overline{b}}{||\overline{a}|| ||\overline{b}||},$
where $||\overline{a}||\;$ is the norm of vector $\overline{a}:\;$ $||\overline{a}||^{2} = \overline{a}\cdot \overline{a}\;$ and similarly for $||\overline{b}||.$
For $\gamma = 90^{\circ},\;$ it follows from the properties of the scalar product that
$||\overline{a} - \overline{b}||^{2} = ||\overline{a}||^{2} + ||\overline{b}||^{2},$
which, in a 2-dimensional case, is easily seen to express the common Pythagorean theorem.
Critique
The problem with this derivation is that the theory of vector spaces is entirely algebraic (or analytic, if you will). Vectors are defined as n-tuples of real numbers which is followed by the componentwise definition of vector operations. Within this framework, the vector Pythagorean identity above is indeed an easy consequence of the axioms and definitions. However, the relationship between the common geometry and the geometry of vector spaces is that of a model and an abstract theory. The above vector identity does not prove the Pythagorean theorem. It only shows that there is a tight relation between the model and the theory. It confirms this relation, perhaps offers an additional insight into the Pythagorean theorem, but does not prove it by any means.
Proof 6
A proof by John Molokach under the caption Calculus Proof for Pythagorean Theorem has been posted on the web. I reproduce the proof on a separate page.
Proof 7
This is a published proof (International Journal of Mathematical Education in Science and Technology, 34:1, 144 - 150) due to Medhat H. Rahim (A new proof of the Pythagorean using a compass and unmarked straight edge).
After a short introduction into the Pythagorean theorem, illustrated by two known proofs, with a short review of the book by E. Loomis, the author proceeds with the proof.
Given two squares $I\;$ and $II,\;$ the author offers a 2-step construction of square $III\;$ such that $[III]=[I]+[II],\;$ where $[F]\;$ denotes the area of shape $F.\;$ The construction is summarized in the following diagram.
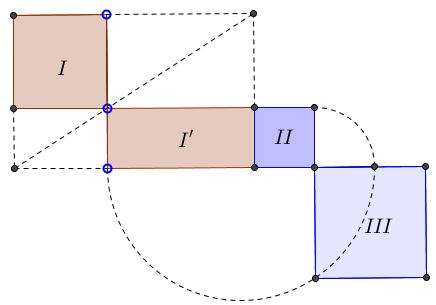
The author shows how to construct a rectangle $(I')\;$ with a given side and satisfying $[I']=[I].\;$ The side chosen is that of $II\;$ which is then placed adjacent to rectangle $I'.\;$ On the second step the author constructs square $III\;$ such that $[III]=[I']+[II].\;$ He then concludes that $[III]=[I]+[II],\;$ as required.
Critique
The article's construction is correct but has nothing to do with proving the Pythagorean theorem.
Proof 8
This proof came in a mail, a short message occampanied by a diagram:
Hello,
I am ready to sacrifice 100 oxen (like the pythagoreans did as per Eli Maor's book on the topic, which I just started reading) if in fact I came up with a "new" proof!! but I doubt that my simple proof has not been proposed before. I have searched internet and so far I haven't encountered a similar proof. I am adding an image file. If your time allows, take a look and give me your opinion please.
Thanks,

Critique
To my objection that the number of strips $\displaystyle\frac{b}{C-a}\;$ is going to be fractional in general, the author replied:
Never mind a number of strips that has a decimal part, what about the fact that according to the World Bank, in Switzerland the total birth per woman is 1 baby and a half!! If we are allowed 0.5 baby we should be ok with having 0.5 or any other decimal or fraction of a strip.
The authors precedes the remark with a detailed calculations for $a=1231,\;$ $b=617,\;$ $C= 1376.971314152913,\;$ getting in particular, $\displaystyle\frac{b}{C-a}=4.226857883554151\text{ strips (NOT AN INTEGER NUMBER)}\;$ and eventually showing that $C^2 = a^2 + b^2\;$ to which I replied that his calculations are valid due to the Pythagorean theorem, no the other way round.
Proof 9
This proof, too, came in a mail, with a later confession of the author that he noticed a mistake after sending the mail, and a suggestion that he hopes that other can learn from his mistake. Here's the rpoof

Critique
Obviously the equation of the circle, say, $x^2+y^2=c^2\;$ assumes the validity of the Pythagorean theorem.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73509122
