Generalizations of the Pythagorean TheoremPythagorean Theorem is one of the most fundamental results of Mathematics. Using the theorem we define what's known as euclidean distance dist2. This notion of distance extends to spaces with scalar product - Hilbert spaces. Proofs ##13, 17, and 18 gave us plane generalizations of the theorem. Below I consider another one, now in the 3-dimensional space R3. The statement leads to the definition of euclidean distance in R3. Afterwards, there is an additional and unexpected analog of the theorem in R3. 
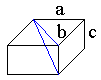
It's convenient to think of the Pythagorean Theorem as defining the length of the diagonal in a rectangle when its
two sides are given. Now consider a parallelepiped with sides a,b, and c. Incidently, the diagonal in question serves
as the hypotenuse of the right triangle formed by the edge c and the diagonal of the face ab. The latter, by the
Pythagorean Theorem, equals When we moved from a 2-dimensional space to a 3-dimensional space the formula for the diagonal of a shape built on orthogonal segments remained virtually the same except the number of terms grew from 2 to 3, as appropriate. However, in both cases squared were line segments. Pythagorean Theorem has an analog where squared are areas of triangles. 
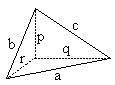
The theorem applies to a special kind of tetrahedra in which all three edges emanating from one of the vertices are perpendicular to each other. One can obtain such a pyramid by cutting a corner from a parallelepiped. Let's introduce areas A,B,C of the faces that house a right angle, and let D be the area of the remaining face. We have
What I want to show is that A² + B² + C² = D². 
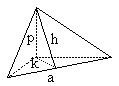
Draw a plane through p perpendicular to a. Then both k and h will be perpendicular to a. We find that
Q.E.D.
Oops, I almost forgot the Cosine Law which is a clear generalization of the Pythagorean Theorem. For a triangle with sides a, b, and c and the angle C opposite the side c, one has
which, in turn, admits a generalization to higher dimensional spaces. The fact expressed nowadays by the single identity appears in Euclid's Elements as two separate propositions: II.12 for obtuse-angled triangles and II.13 for the acute ones. Dr. Scott Brodie from the Mount Sinai School of Medicine, NY, sent me a proof of the theorem and a dynamic Geometer's SketchPad illustration.
References
|Contact| |Front page| |Contents| |Store| |Generalizations| |Geometry| Copyright © 1996-2012 Alexander Bogomolny |
. Applying it the second time gives the length of the
diagonal as 
.
| 40601111 |
