PLC: Apollonius Problem with a point, a line, and a circle

Below I give an Euclidean construction to a variant of the Problem of Apollonius:

Find a circle tangent to a given line \(m\), circle \((A)\), and passing through a given point \(B\):

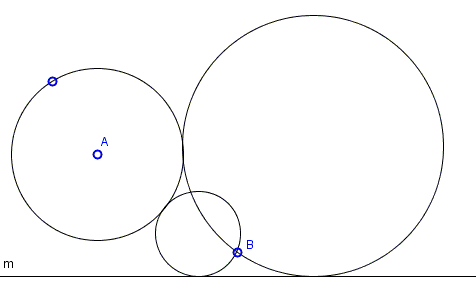
Construct a circle tangent to a given line, a given circle, and passing through a given point

(The applet below illustrates the construction. Points \(A, B\) and line \(m\) are draggable. This permits changing the configuration, but within certain limitations.)

Solution

Construction

Find a circle tangent to a given line \(m\), circle \((A)\), and passing through a given point \(B\):

Construct a circle tangent to a given line, a given circle, and passing through a given point

Let's analyze the problem assuming that a solution has been found. Assume there is a circle through \(O\) through \(B\) that touches \(m\) at \(P\) and \((A)\) at \(L:\)

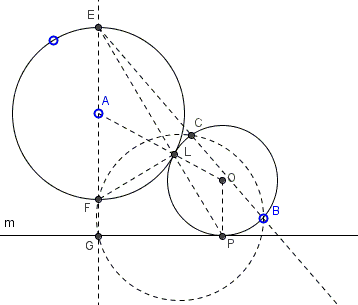
analysis of Apollonius' problem with a point, a line, and a circle

Note that \(OP\perp m\). Let \(EF\) be the diameter of \((A)\) perpendicular to \(m\). Point \(L\) of tangency of the two circles serves as their center of similitude so that, besides lying on \(AO\) it also belongs to (in the diagram) \(EP.\) Since \(EF\) is a diameter, \(\angle ELF\) is right, as is \(\angle EGP\), making quadrilateral \(FLPG\) cyclic. By the Intersecting Secants Theorem,

\( EF\cdot EG = EL\cdot EP = EB\cdot EC \)

where \(C\) is the second point of intersection of \(EB\) with \((O)\). By the inverse of the Intersecting Secants Theorem, quadrilateral \(FCBG\) is cyclic, such that \(C\) can also be determined as the intersection of \(EB\) and \((FCBG)\). Thus circles that solve the problem pass through two point \(B\) and \(C\) and are tangent to either \(m\) or \((A)\). The PLC problem is thus reduced to a choice of either PPL or PPC.

The construction starts with finding \(C\) and continuing with one of the PPL or PPC constructions, does not matter which. Either leads to two solutions. Swapping the roles of \(E\) and \(F\) leads to two more solutions, making the total number of solutions 4.

The construction does not work when \(m\) separates \(B\) and \(C\), or when \(B\) lies on \(EF,\) although, in the latter case, two solutions may exist when \(G\not\in EF\) while \(B\in FG.\)

References

N. Altshiller-Court, College Geometry, Dover, 1980, #512

71942547