Directly Similar Figures: What is that about?
|
| Buy this applet What if applet does not run? |
|Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
Explanation
The applet suggests the following statment:
| (1) | Given two similar triangles ABC and A'B'C' and a point P, let A1 = P + AA', B1 = P + BB', and C1 = P + CC'. Then triangle A1B1C1 is similar to ABC and A'B'C'. |
| Buy this applet What if applet does not run? |
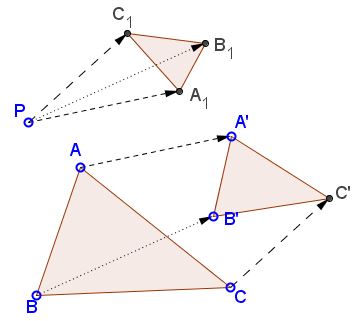
The statement implies something more general, akin to the Fundamental Theorem of Directly Similar Figures and relates to the properties of spiral similarities. For any two directly similar figures S and S', if A is a generic point of S and A' is the corresponding point of S', then for any point P,
The proof (in complex numbers) follows easily from
 |
with m = 1 and l = -1.
References
- I. M. Yaglom, Geometric Transformations II, MAA, 1968
|Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 40585852 |
