Triangle from Side, Circumradius, and Median
There are two essentially different combinations of the circumradius, a side and a median. In one the median is to the given side, in the other it's to any of the remaining two. We shall consider the two cases separately.
In both case we may assume that a circle, say, $(O)=C(O,R)$ of radius $R$ and its chord $BC$ are given.
Triangle from $R,$ $a,$ $m_a$
Construct $\Delta ABC,$ given side $BC=a,$ the circumradius $R,$ and the median $m_a.$
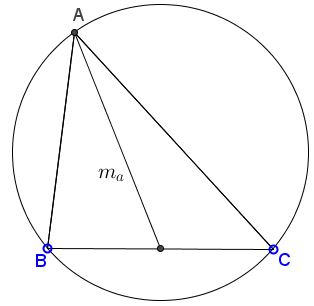
Construction
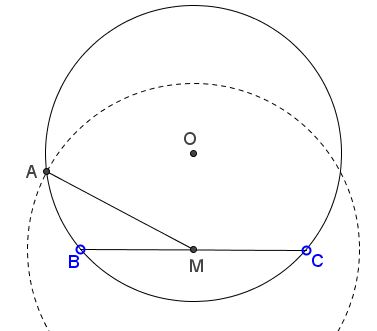
If $M$ is the midpoint of $BC$ then any intersection of circle $C(M,m_a)$ with $(O)$ will legitimate serve as vertex $A$ of $\Delta ABC.$
Triangle from $R,$ $a,$ $m_b$
Construct $\Delta ABC,$ given side $BC=a,$ the circumradius $R,$ and the median $m_b.$
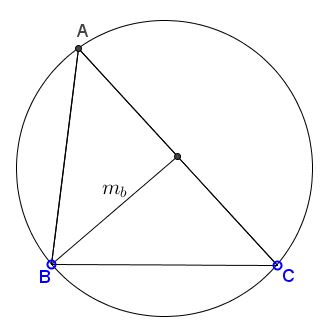
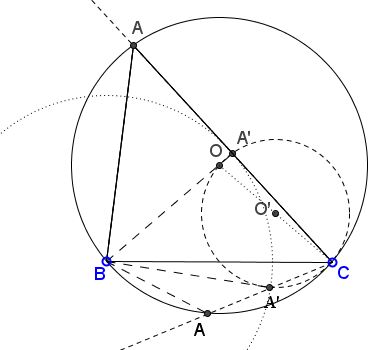
Construction
Let $O'$ be the midpoint of $OC.$ The midpoint of side $AC$ of $\Delta ABC$ is bound to lie on $(O')=C(O', R/2),$ the circle with center $O'$ and Radius $R/2.$ This midpoint is simultaneously at distance $m_a$ from B. If $A'$ is the intersection of $(O')$ and $C(B,m_A )$ (there may be 0, 1, or 2 points of intersection), then $A'$ is the midpoint of $AC$ so that $A$ can be found on $A'C$ as the intersection of the latter with $(O).$
Acknowledgment
I was alerted to a gap in the collection of triangle constructions by Prof. Dr. René Sperb who sent me the second of the two constructions. I added the first one for the sake of completeness.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73582490
