The many ways to construct a triangle IV

Constructions by Jacopo (Jack) D'Aurizio

m_a, m_b, c
Since the medians cut themselves in a 2/3-ratio, this is a SSS problem.
m_a, m_b, b
For the same reason, this is a SSS problem with side lengths (2m_a/3 , b/2 , m_b/3).
R, h_a, a
Draw an isosceles triangle with side lengths (R,R,a) and vertex O. Cut the circumcircle with a line parallel to a at distance h_a.
R, m_a, a
Draw an isosceles triangle with side lengths (R, R, a) and vertex O. Draw a circle with center in the midpoint of a and radius m_a and intersect it with the circumcircle.
A, a, m_a
Draw the circle that sees a under an angle equal to A. Intersect it with a circle centered in the midpoint of a having radius m_a.
A, B, h_c
Draw the altitude h_c and a line l perpendicular to it. Draw the circles that see h_c under angles equal to B,C and intersect them with l.
A, h_a, l_a
Draw a right triangle having side lengths h_a, l_a, sqrt(l²_a - h²_a). Intersect the last side with the lines forming angles equal to +A/2 ,-A/2 with l_a.
A, a, r
The distance between I and a is r, the angle ∠BIC is (pi+A)/2, so we can solve the problem by intersecting a circle and a line parallel to a.
m_a, h_a, h_b
We draw a circle having m_a as diameter, then intersect it with two circles centered in the endpoints of m_a and having radii equal to h_a, h_b/2.

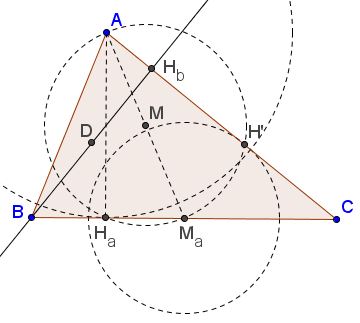
In this way we determine the feet h_a of the altitude h_a and the direction of the side b, so we find the vertex C, then the vertex B.
m_a, h_b, h_c
We draw two opposite right triangles sharing a common hypotenuse m_a and having sides opposite to vertex A with lengths h_b/2, h_c/2. In this way we determine the lines containing the sides (b, c), having only to find two points on these lines with the proper distances (h_c, h_b) from (b, c).
m_a, h_a, m_b
We draw a right triangle having side lengths (h_a, m_a, sqrt(m_a² - h_a²)). We call l the line containing the last side, and G the point on m_a such that 3 AG = m_a. We intersect a circle centered in G with radius 2m_b/3 with the line l, finding B, then C.
m_a, m_b, h_c
We glue two right triangles such that the triangle GAB satisfies
- GA = 2m_a/3
- GB = 2m_b/3
- d(G, AB) = h_c/3
then call (U, V) the midpoints of (GA, GB). We call m_a the symmetric of U with respect to G, and m_b the symmetric of V with respect to G. Am_b and Bm_a concur in C.
a, h_b, R
We draw an isosceles triangle with side lengths (R, R, a) and vertex O. We draw a circle having a as a diameter, and find a point h_b on it such that BH_b = h_b. The intersection of the line CH_b with the circumcircle is A.
h_a, l_a, b
We build a triangle ACH_a having AC = b, AH_a = h_a, CH_a perpendicular to AH_a. On the line CH_a we determine l_a such that AL_A = l_a. We call D the symmetric of C with respect to the line Al_a. The intersection of AD and CL_A is B.
A, h_a, h_b
We build a right triangle ABH_b having AH_b = h_b, ∠BAH_b = A, AH_b perpendicular to BH_b. We find a point h_a such that BH_a is perpendicular to AH_a and AH_a = h_a by drawing the circle having AB as a diameter. The intersection of BH_a and AH_b is C.
m_a, h_a, l_a
We draw M_a, H_a and L_a such that they lie on a line l perpendicular to AH_a and satisfy AH_a = h_a, AM_a = m_a, AL_a = l_a. We intersect the perpendicular to l through M_a (the perpendicular bisector of BC) with the line AL_a, finding E, that is the midpoint of the arc BC in the circumcircle (little folklore apart: in the Italy IMO team this fact is generally called "Tiozzo's lemma", from the great contestant Giulio Tiozzo). The intersection of the perpendicular bisector of AE with the line EM_a is O, the circumcenter. So we draw the circumcircle with radius OA and find B and C on l.

72393954