Triangle from Side, Median, and Altitude
There are essentially five different combinations {side, altitude, median} and, accordingly, five different constructions.
Triangle from $a,$ $h_a,$ $m_a$
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_a,$ and the median $m_a.$
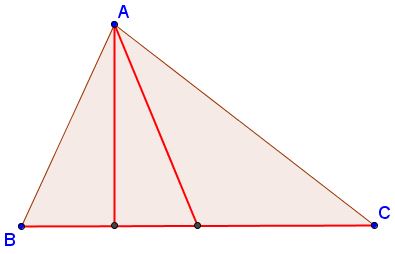
Construction
Construct $\Delta AM_{a}H_{a}.$ Line $M_{a}H_{a}$ determines the base of the triangle whose middle point coincides with $M_{a}.$ From $M_{a}$ measure $a/2$ in both directions to obtain points $B$ and $C.$
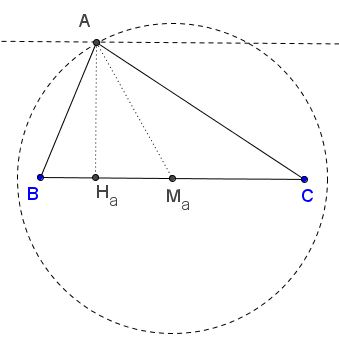
Another construction (Jacopo D'Aurizio): Place $BC=a$ on the plane; draw a line parallel to $BC$ at distance $h_{a}$ from it; next intersect the line with a circle centered in the midpoint $M_a$ of radius $m_{a}.$
Triangle from $a,$ $h_a,$ $m_b$
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_a,$ and the median $m_b.$
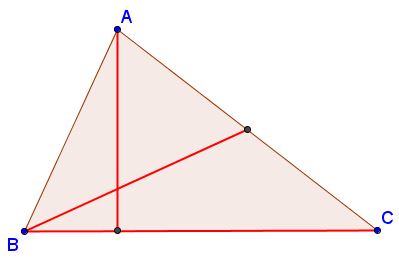
Construction
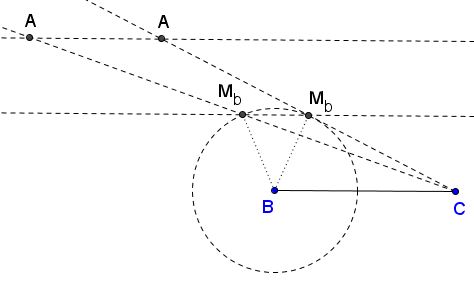
Draw line $l$ parallel to $BC=a$ at distance $h_a$ from the latter and another parallel line $m$ midway between the first two. Intersect $m$ with the circle $C(B,m_b)$ centered at $B$ with radius $m_a$ to find $M_b$ - the midpoint of $AC.$ (There could be two, one, or no intersections.) Extend $CM_b$ to the intersection with $l$ at $A.$
Triangle from $a,$ $h_b,$ $m_a$
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_b,$ and the median $m_a.$
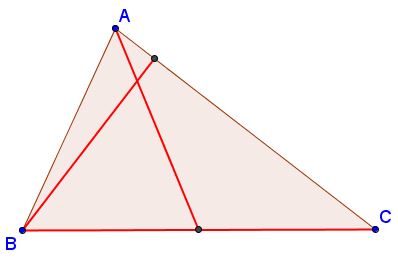
Construction
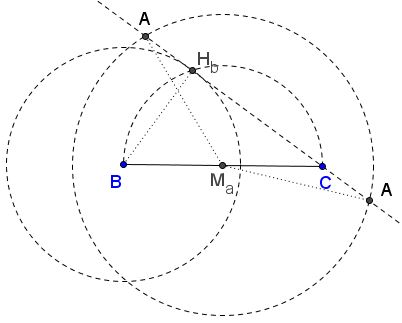
Draw circle, say, $\omega$ with $BC$ as diameter and intersect it with circle $C(B,h_b)$ to find $H_b$ as the intersection of the two. $BH_{b} = h_{b},$ $BC = a.$ Next, draw a circle centered in the midpoint $M_a$ of $BC$ having radius $m_{a},$ then intersect it with $CH_{b}$ to find $A.$ The problem may have two, one, or no solution.
Triangle from $a,$ $h_b,$ $m_b$
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_b,$ and the median $m_b.$
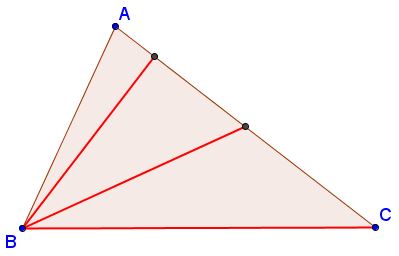
Construction
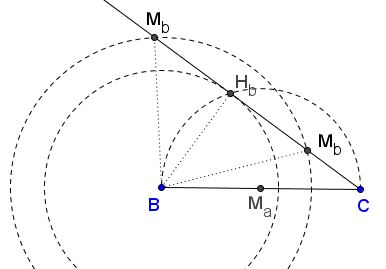
Draw circle, say, $\omega$ with $BC$ as diameter and intersect it with circle $C(B,h_b)$ to find $H_b$ as the intersection of the two. Extend $CH_{b}$ beyond $H_{b}.$ From $B$ sweep and arc of radius $m_{b}.$ It will intersect $CH_b$ in $M_b.$ Several cases are possible. If $m_{b}$ is too short to reach the line, there is no solutions. If $m_{b} = h_{b},$ there is a single solution and the triangle is isosceles. The diagram depicts the case of two solutions.
Once $M_b$ is known, extend $CM_b$ to twice its length to locate $A.$
Triangle from $a,$ $h_b,$ $m_c$
Construct $\Delta ABC,$ given side $BC=a,$ the altitude $h_b,$ and the median $m_c.$
Construction
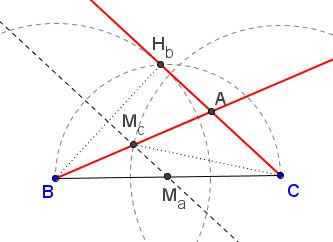
As before, construct right $\Delta BCH_b.$ Through the midpoint $M_a$ of $BC$ draw the line $l$ parallel two $CH_b.$ Intersect circle $C(C,m_c)$ centered at $C$ with radius $m_c$ with $l$ to obtain $M_c.$ Consider how many solutions are possible. $A$ is found at the intersection of $BM_c$ and $CH_b.$
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73579590
