A Problem of Two Incircles by Miguel Ochoa Sanchez
Source
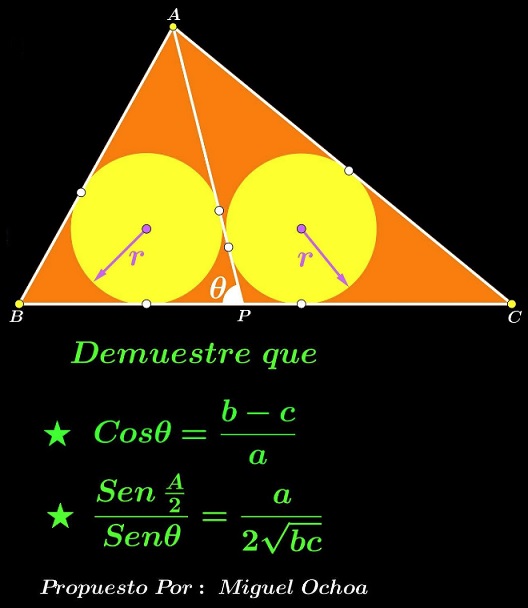
Problem
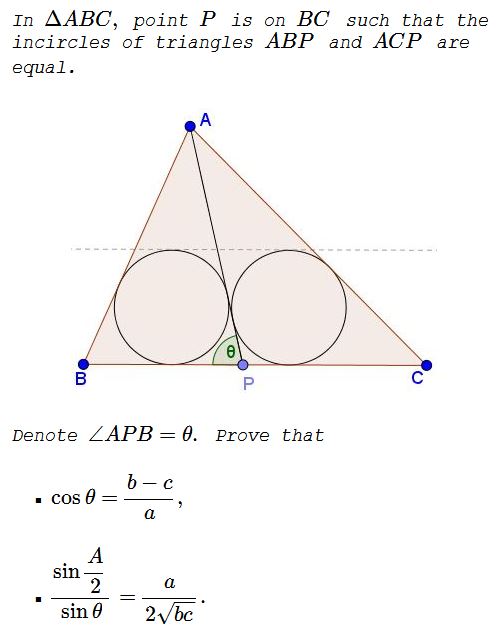
Solution 1
Denote $AP=x.\,$ We have $2[\Delta ABP]=h_a\cdot BP=r(BP+c+x)\,$ and $2[\Delta ACP]=h_a\cdot CP=r(CP+b+x).\,$ Thus
$\displaystyle \frac{BP}{CP}=\frac{BP+c+x}{CP+b+x}\,\Rightarrow\,\frac{BP}{CP}=\frac{c+x}{b+x}\,\Rightarrow\, PC=\frac{a(b+x)}{b+c+2x}.$
Also, if $p\,$ is the semiperimeter of $\Delta ABC,\,$ $p_1\,$ and $p_2\,$ are semiperimeters of triangles $ABP\,$ and $ACP,\,$ respectively, then
$\displaystyle p_1=\frac{(c+x)(p+x)}{b+c+2x}\,$ and $\displaystyle p_2=\frac{(b+x)(p+x)}{b+c+2x}.$
In $\Delta ABP,\,$ $\displaystyle \cos\frac{\theta}{2}=\sqrt{\frac{p_1(p_1-c)}{x\cdot BP}}\,$ and, since $\displaystyle \cos\frac{\theta}{2}=\sqrt{\frac{1+\cos\theta}{2}},\,$ we need to show that $\displaystyle\frac{p_1(p_1-c)}{x\cdot BP}=\frac{p-c}{a}.$
Explicitly,
$\displaystyle \frac{p_1(p_1-c)}{x\cdot BP}=\frac{\displaystyle \frac{(c+x)(p+x)[x^2+(p-c)x-c(p-a)]}{(b+c+2x)^2}}{\displaystyle x\cdot\frac{a(c+x)}{b+c+2x}}.$
Thus remains it to show that
$\displaystyle \begin{align} &(p+x)[x^2+(p-c)x-c(p-a)]=x(p-c)(b+c+2x),\,\text{i.e.,}\\ &(x+c)(x^2-p(p-a))=0. \end{align}$
Now, in $\Delta ABP,\,$ for the inradius $r,\,$ $\displaystyle r^2=\frac{(p_1-c)(p_1-x)(p_1-BP)}{p_1};\,$ and in $\Delta ACP,\,$ $\displaystyle r^2=\frac{(p_2-b)(p_2-x)(p_2-CP)}{p_2}.\,$ With a relatively straightforward effort, the resulting equation reduces to $(x+2p-a)(x^2-p(p-a))=0\,$ from which $x^2=p(p-a).$
The second part is trivial.
Solution 2
Lemma
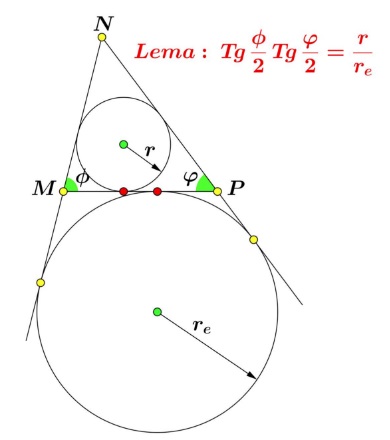
Applying the lemma in $\Delta ABP\,$ we get
$\displaystyle\begin{align} &\tan\frac{B}{2}\tan\frac{\theta}{2}=\frac{r}{r_e}=\tan(90^{\circ}-\frac{\theta}{2}\tan\frac{C}{2}\,\Rightarrow\\ &\tan^2\frac{\theta}{2}=\frac{\displaystyle \tan\frac{C}{2}}{\displaystyle \tan\frac{B}{2}}=\frac{p-b}{p-c}\,\Rightarrow\\ &\tan^2\frac{\theta}{2}=\frac{p-b}{p-c}. \end{align}$
(Here we used P. Yiu's observation (Missouri J. Math. Sci., 15 (2003) 21-32) to the effect that if the cevian $AP$ has, as stipulated in the problem, the property that the inradii of triangles $ABP$ and $ACP$ are equal, then so are the radii of their excircles opposite vertex $A.)$
Now, concerning the first question,
$\displaystyle \cos\theta=\frac{\displaystyle 1-\tan^2\frac{\theta}{2}}{\displaystyle 1+\tan^2\frac{\theta}{2}}=\frac{\displaystyle 1-\frac{p-b}{p-c}}{\displaystyle 1+\frac{p-b}{p-c}}=\frac{b-c}{a},$
i.e., $\displaystyle \cos\theta=\frac{b-c}{a}.\,$ Concerning the second question,
$\displaystyle \sin\theta=\frac{\displaystyle 2\tan^2\frac{\theta}{2}}{\displaystyle 1+\tan^2\frac{\theta}{2}}=\frac{2\sqrt{(p-b)(p-c)}}{a},$
so that
$\displaystyle \frac{\displaystyle \sin\frac{A}{2}}{\displaystyle \sin\theta}=\frac{\displaystyle \sqrt{\frac{(p-b)(p-c)}{bc}}}{\displaystyle 2\frac{\sqrt{(p-b)(p-c)}}{a}}=\frac{a}{2\sqrt{bc}}.$
Thus, $\displaystyle \frac{\displaystyle \sin\frac{A}{2}}{\displaystyle \sin\theta}=\frac{a}{2\sqrt{bc}}.$
Extension (IMO 1988 short list)

Acknowledgment
The statement is due to Miguel Ochoa Sanchez. I am grateful to Leo Giugiuc who posted the problem and a solution of his (Solution 1) at the CutTheKnotMath facebook page. Solution 2 is by Miguel Ochoa Sanchez who also added the extension part.
Note that in the process, both solutions gave an answer to a related sangaku.
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573323
