Triangle from Angle Bisector, Altitude and Circumradius
Construct $\Delta ABC,$ given angle bisector $l_a,$ altitude $h_a,$ and circumradius $R.$
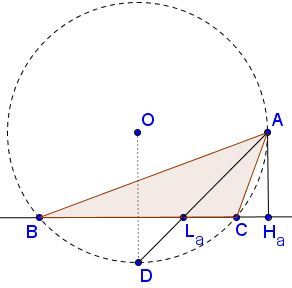
Analysis
The angle bisector and the altitude from the same vertex $A$ define uniquely $\Delta AL_{a}H_{a}.$ The circumradius would be useful if we knew the circumcenter $O.$ The circumcenter $O$ lies at the intersection of circle $C(A,R),$ with center $A$ and radius $R,$ and the perpendicular to $L_{a}H_{a}$ through $D,$ the point where the angle bisector meets the circumcircle the second time. The perpendicular bisector of $AD$ also passes through $O.$
The circumcenter also lies at
Construction
Draw $\Delta AL_{a}H_{a}$ and arbitrarily choose point $P$ on the extended angle bisector $AL_a.$ Let $Q$ be the intersection of the perpendicular to $L_{a}H_{a}$ through $P$ and the perpendicular bisector of $AP.$

Then the intersection $O$ of $AQ$ and $C(A,R)$ is the circumcenter of soon-to-be $\Delta ABC.$ Find $B$ and $C$ at the intersection of $L_{a}H_{a}$ with the circle $C(O,R),$ with center $O$ and radius $R.$
Proof
Assuming the triangle $ABC$ exists (this requires at least $l_{a}\ge h_{a},)$ we found $Q$ at the intersection of perpendicular from $P$ to $L_{a}H_{a}$ and the perpendicular bisector of $AP.$ Apply homothety $h$ centered at $A$ with coefficient $R/AQ.$ Let $D=h(P)$ and $O=h(Q).$ Note that this makes triangles $APQ$ and $ADO$ similar and, since $AQ=PQ,$ $AO=DO=R.$ In particular, $O$ lies on $C(A,R).$
Of course, $DO\perp L_{a}H_{a}$ because, by the construction, $DO\perp L_{a}H_{a}.$ Hence points $B$ and $C$ are equidistant from $D$ which makes $D$ the midpoint of the arc of $C(O,R)$ subtended by the chord $L_{a}H_{a}$ and $AL_{a}D$ the bisector of angle $BAC.$
Acknowledgment
The construction was communicated to me by Prof. Dr. René Sperb.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73537942
