Triangle from Two Side Lines and the Euler Line

Construct $\Delta ABC,$ given side lines $aa$ (through $B$ and $C)$ and $bb$ (through $A$ and $C)$ and the Euler line $e$ of $\Delta ABC.$

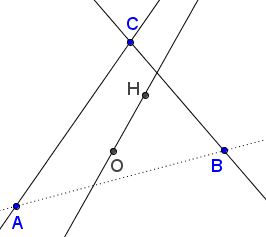
Triangle from Two Side Lines and the Euler Line - problem

Construction 1

Let $C$ denote the intersection of $aa$ and $bb,$ $M$ and $N$ the intersections of these lines with $e.$ Let $e'$ be the Euler line of $\Delta CMN.$ Then, as it was shown elsewhere, $e'\parallel AB.$

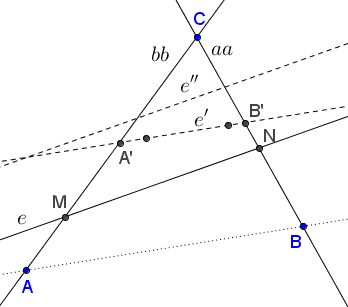
Triangle from Two Side Lines and the Euler Line - Construction 1

Let $A'$ and $B'$ be the intersections of $e'$ with $bb$ and $aa,$ respectively. Find $e''$ - the Euler line of $\Delta A'B'C.$ By the above, $e''\parallel e$ such that there is a unique homothety with center at $C$ that maps $e''$ onto $e.$ This homothety maps $A'B'$ onto $cc.$

Construction 2

This is an analytic variant of the previous construction. It is especially interesting due to a formula it is based on:

Assume the side lines $aa,bb,cc$ and the Euler line $e$ of $\Delta ABC$ have slopes $m_a,\,m_b,\,m_c,\,m_e,$ respectively. Then

$\begin{align} m_{a}m_{b} + m_{a}m_{c}+ m_{a}m_{e} + m_{b}m_{c}&+ m_{b}m_{e} + m_{c}m_{e}\\ &+ 3m_{e}m_{a}m_{b}m_{c} + 3 = 0. \end{align}$

This is Lemma 1 from Gossard’s Perspector and Projective Consequences by W. G. Boskoff, L. Homentcovschi, and B. D. Suceava (Forum Geometricorum, Volume 13 (2013) 169–184). The article is a follow-up on a problem in the 2003 Monthly dealt with elsewhere.

The identity shows clearly that $m_c$ is uniquely determined from the other three slopes. Knowing $m_c$ reduces the construction to the previous one.

The above identity is remarkable in that it is symmetric with respect to all four slopes involved. As was noted by Boskoff et al, this means that if, in the triangle formed by some three of the four given lines, the Euler line is parallel to the omitted line, the same holds for the other three triangles obtained by omitting the remaining three lines - one at a time. This solves the problem 10980 from the Mathematical Monthly (Dec 2002, v 109, N 10, p. 921) proposed by Ye Zhong HaoWu Wei Chao.

Construction 3

Given the lines $aa,$ $bb$ (we don't know $A$ or $B,$ only $C),$ and the Euler line $e,$ we take an arbitrary point $O'$ on $e,$ and find points $B'$ on $aa$ and $A'$ on $bb$ such $O'$ serves as the circumcenter of $\Delta A'B'C.$ Next we get the orthocenter $H'$ of $\Delta A'B'C.$ Fortunately, the locus of $H'$ is a line, and the intersection of this line and $e$ gives the orthocenter $H$ of the sought triangle. To determine the locus we repeat the previous steps with a different point $O''$ on $e,$ thus getting $H''$ such that $H'H''$ is the required locus.

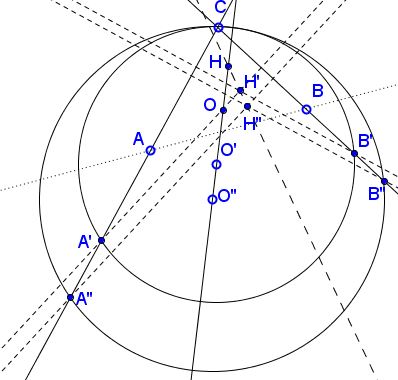
Triangle from Two Side Lines and the Euler Line - Construction 3

Construction 4

Let $Y$ be the intersection of $e$ with $aa,$ $Z$ the intersection with $bb.$ Drop perpendiculars $YM$ to $aa$ and $ZN$ to $bb$. Define $Y'$ as the reflection of $C$ in $M;$ $Z'$ the reflection of $C$ in $N.$ Line $Y'Z'$ intersects $e$ in $H.$

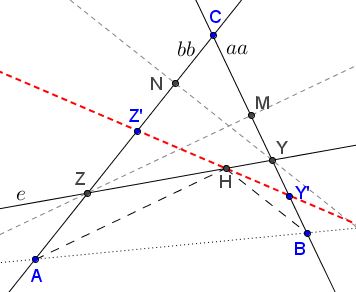
Triangle from Two Side Lines and the Euler Line - Construction 4

Construction 5

Reflections of the Euler line in the side lines $aa$ and $bb$ cross on the circumcenter (point $E$ below, Collings' Theorem).

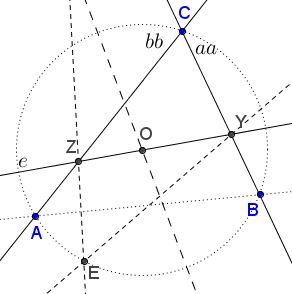
Triangle from Two Side Lines and the Euler Line - Construction 5

The perpendicular bisector of $E$ and, say $B,$ cross the Euler line in the circumcenter $O$ of the sought triangle. The circle with center $O$ through $A$ crosses $bb$ and $aa$ in $A$ and $B.$

Acknowledgment

The question whether two side lines and the Euler line of a triangle determine the triangle uniquely has been posted by Oai Thanh Dao at the CutTheKnotMath facebook page. Constructions 3 and 4 are by Francisco Javier García Capitán; construction 5 is by Antreas Hatzipolakis.

71544717