Triangle from Angle, Inradius, and Difference of Sides
Construct $\Delta ABC,$ given angle $A=\angle BAC,$ the inradius $r,$ and the difference $c-a,$ where, as usual, $c=AB$ and $a=BC.$
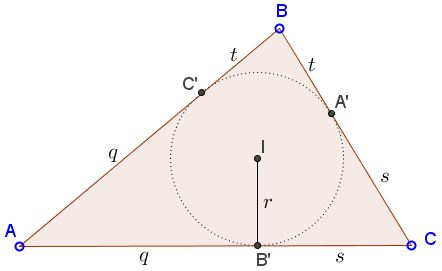
(Note that this assumes that $AB\gt BC.)$
Analysis
Let $A',B',C'$ denote the points of tangency of the incircle with the sides of $\Delta ABC,$ as above. Let also,
$\begin{align} AB'&=AC'=q,\\ BA'&=BC'=t,\\ CA'&=CB'=s. \end{align}$
Then $c-a=(q+t)-(s+t)=q-s.$ This makes point $P$ on $AC$ at distance $q-s$ equidistant with $C$ from $B',$ making the following construction natural.
Construction
Draw angle $A$ and inscribe into it a circle of radius $r:$
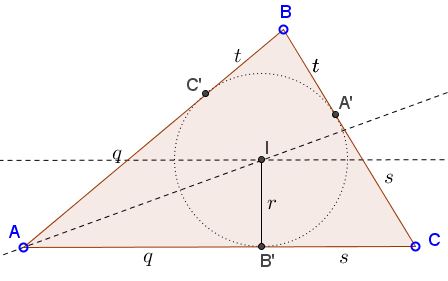
Given that, mark point $P$ on $AC$ at distance $c-a$ from $A.$ Draw circle $C(B',P)$ centered at $B'$ through $P.$
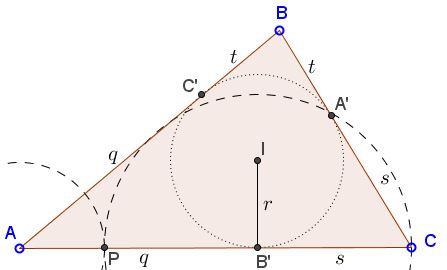
Its second intersection with $AC$ is at $C.$ Drawing tangents to the incircle from $A$ and $C$ gives the remaining vertex $B.$
Acknowledgment
The construction was communicated to me by Prof. Dr. René Sperb.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73569767
