Tiling Sphere by Four Equal Triangles
The following statement is truly obvious:
Projections of the edges of an isosceles tetrahedron from its circumcenter onto the circumsphere tile the sphere with equal spherical triangles.
The area of a sphere is known to be $4\pi R^2,$ where $R$ is the radius of the sphere. If the circumradius of the tetrahedron is taken to be $1,$ the area of its circumsphere becomes $4\pi$ so that each of the four triangles has area of $\pi.$ The converse of that would say that any tiling of the sphere by four equal triangles define an inscribed isosceles tetrahedron. But more is true.
Theorem 1
For any spherical triangle of area $\pi$ on the unit sphere, four congruent copies of it tile the sphere; that is, the copies can be positioned so that any two triangles meet at an edge, with vertices meeting vertices, and the union of these four triangles is the sphere.
As a consequence, we have
Theorem 2
Any spherical triangle of area $\pi$ on the unit sphere defines uniquely - by means of the four vertices of the associated tiling - an inscribed isosceles tetrahedron.
The two theorem are the subject of a 2005 article by Jeff Brooks and John Strantzen which is available online at the official site of Mathematics Magazine where it was published. Theorem 1 is based on Girard's formula for the area of a triangle on a unit sphere. For a spherical $\Delta ABC,$ with angles $\alpha,\beta,\gamma$
$\alpha+\beta+\gamma-\pi=Area(\Delta ABC),$
an elegant proof of which can be found in [Weeks, 137-143]. The proof of Theorem 1 is illustrated by the following diagram
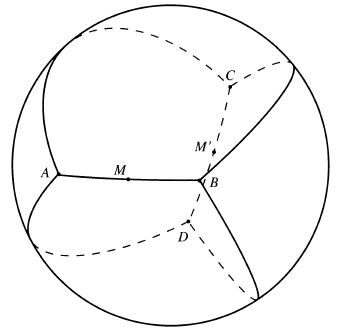
which, according to the authors, practically gives the proof away.
Lest you think that the result is overly simple, ponder this: due to Girard's formula, similarity on a sphere means congruence. What is naturally true in a plane, does not often translates onto the sphere. For example, the fact that a plane triangle is getting split into four identical (but smaller) copies of itself by the medial lines has no analogue on the sphere. In particular, if the splitting is done on the faces of an isosceles tetrahedron and the small triangles projected from the circumcenter onto the circumsphere, the result won't be a tiling of the sphere with sixteen copies of congruent triangles.
References
- Jeff Brooks and John Strantzen, Spherical Triangles of Area $\pi$ and Isosceles Tetrahedra, Mathematics Magazine, Vol. 78, No. 4 (Oct., 2005), pp. 311-314
- Jeffrey R. Weeks, The Shape of Space, 2nd ed., Marcel Decker, Inc., New York, Basel, 2002.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579670
