Similar Parallelograms on Sides of a Triangle
Problem
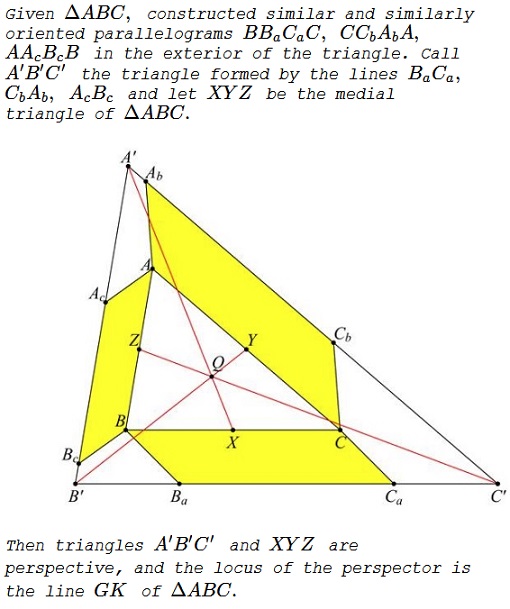
Solution
We use barycentric coordinates and Conway's notations. Let $S\,$ be twice the area of $\Delta ABC.\,$ Call $\lambda=\cot\angle CBB_a,\,$ $\mu=\cot\angle BCB_a.\,$ Then we have point $B_a=(-a^2:S_C+S\mu:S_B+S\lambda).\,$ Since the parallelograms are similar, we have the same angles for the other sides and we can calculate the points $C_b=(S_B+S\lambda:-b^2:S_A+S\mu)\,$ and $A_c=(S_B+S\mu:S_A+S\lambda:-c^2).$
Now we calculate the points
$\begin{align} A' &= (b^2+c^2+S(\lambda+\mu):-b^2:-c^2),\\ B' &= (-a^2:a^2+c^2+S(\lambda+\mu):-c^2),\\ C' &= (-a^2:-b^2:a^2+b^2+S(\lambda+\mu)) \end{align}$
and the intersection point of $A'X,\,$ $B'Y,\,$ and $C'Z:\,$
$Q=(b^2+c^2+(\lambda+\mu)S:c^2+a^2+(\lambda+\mu)S:a^2+b^2+(\lambda+\mu)S).$
This point $Q\,$ divides the segment $GK\,$ in the ratio
$\displaystyle \frac{GQ}{QK}=-\frac{a^2+b^2+c^2}{3(a^2+b^2+c^2+S(\lambda+\mu))}.$
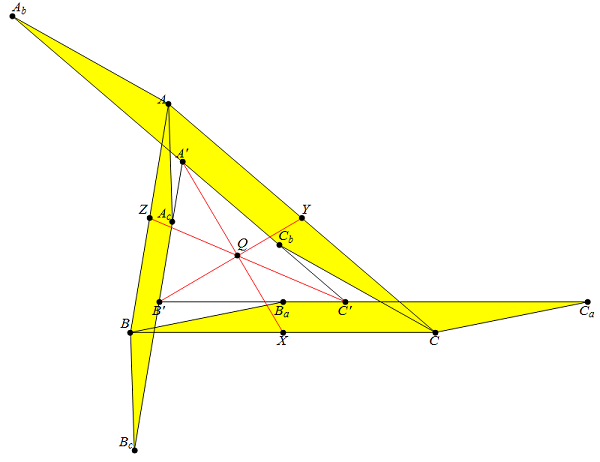
The proof holds for the parallelograms all drawn towards the interior of the triangle as well as in the exterior, because the angles involved could be considered signed:
Acknowledgment
The problem has been originally proposed by Kadir Altintas and posted by Takis Chronopoulos at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group:
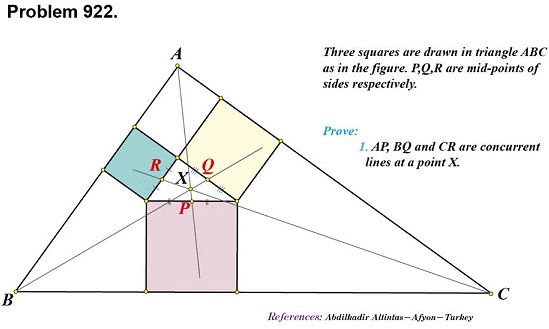
It was later upgraded to the case of similar and similarly oriented parallelograms. Kostas Theodoros Rekoumis has observed that the problem of concurrence is solved in a one step reference to Desargues' theorem even when the parallelograms are not necessarily similar. The above extension of the problem and the solution are due to Francisco Javier García Capitán.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73578739
