Construction of Triangle from Side, Angle, and that Angle's Bisector

Construct a triangle, given side $a,$ the opposite angle $A$, and the angle bisector $l_a.$

Construction

|Contact| |Front page| |Contents| |Up|

Prof. Dr. René Sperb
19 September 2014

Construct a triangle, given side $a,$ the opposite angle $A$, and the angle bisector $l_a.$

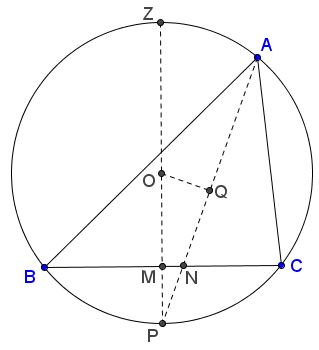
Triangle by side, angle, and angle bisector - problem

Starting from the end, let $O$ be the circumcenter of $\Delta ABC,$ $M$ the midpoint of $BC,$ $P$ the midpoint of the arc subtending $\angle BAC,$ and $OQ\perp AP,$ with $Q$ on $AP,$ $N$ the intersection of $BC$ and $AP.$

The problem is solved if we can construct the length of $PN.$ To this end we set $PN = s,$ $PM = h$ and use the fact that triangles $MNP$ and $QOP$ are similar. This yields the relation

$\displaystyle\frac{l_{a }+ s}{2R} = \frac{h}{s},$

where $R$ is the circumradius of $\Delta ABC:$ $R=OP.$ In other words, $2Rh = (l_a + s ) s.$

At this point we may use the Intersecting Secants Theorem to find $s$ from the last equation.

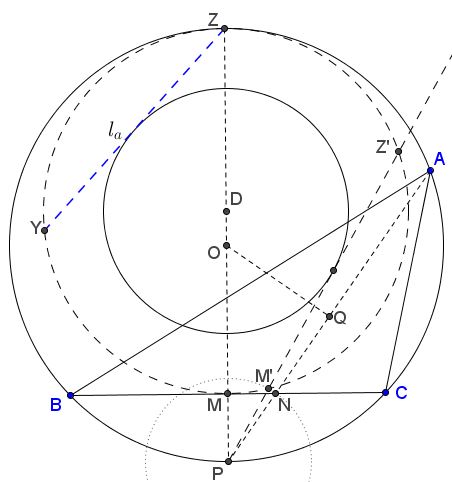
Triangle by side, angle, and angle bisector - construction

Form circle $(D)$ with $MZ$ as diameter ($Z$ being the antipode of $P$ on $(O).)$ Find $M'$ on $(D)$ such that $PM'=PN$ and let $Z'$ be the second intersection of $PM'$ and $(D).$ For the circle $(D)$ one has

$PZ\cdot PM = PM'\cdot PZ',$

or, $2Rh=s\cdot PZ',$ making $PZ'=s+l_a$ and, therefore, $M'Z'=l_a.$

This leads to the following construction:

  1. Construct circle $(O)$ with $BC=a$ as a chord subtending angles $A.$ Let $P$ be the midpoint of the opposite arc, $M$ the midpoint of $BC,$ $Z$ the antipode of $P$ on $(O).$

  2. Cut a chord, e.g., $YZ$ equal in length to $l_a.$

  3. Let $D$ be the midpoint of $MZ,$ $(D)$ the circle on diameter $MZ$ and $\overline{(D)}$ the circle with center $D$ tangent to $YZ.$

  4. Draw tangent from $P$ to $\overline{(D)}$ and let it cross $(D)$ at $M'.$

  5. Find $N$ on $BC,$ with $PN=PM'$ and chord $PA$ of $(O)$ passing through $N,$ or $PA=PZ'.$

This gives $A$ as the sought vertex of $\Delta ABC.$ To prove that reverse the steps leading to the construction.

The construction may not be always possible. This happens if $l_a$ is "too long," i.e. longer than $MZ.$

|Contact| |Front page| |Contents| |Up|

Copyright © 1996-2018 Alexander Bogomolny

72185090