Construction of a Triangle from the Circumradius, Inradius, and an Altitude
Jack D'Aurizio
9 July, 2016
Let we start by drawing the circumcircle $\Gamma\;$ with centre at $O\;$ through $A,\;$ with $OA=R.\;$ Given some $P\;$ such that $AP=h_A\;$ (a candidate feet of the $A$-altitude), the perpendicular to $AP\;$ through $P\;$ meet $\Gamma\;$ at $B',C'.\;$ We have the following
Lemma
As $P\;$ varies on the circle $C(A,h_A),\;$ the intersection $I'\;$ of the bisectors of $\angle AB'C'\;$ and $\angle AC'B'\;$ traces a circle.
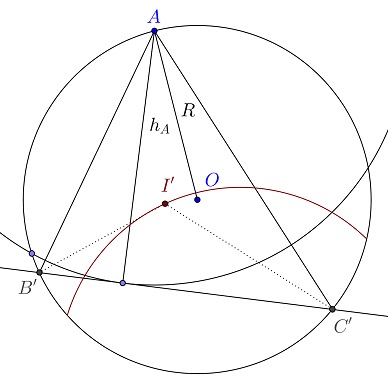
A proof of the lemma is available elsewhere.
To continue, since we know $R\;$ and $r\;$ we also know $OI\;$ by Euler's theorem, hence the incenter has to lie on the previous circle and on some circle centered at $O\;$ with radius $R^2-2Rr.\;$ Given $A,O,R,h_A\;$ and $I,\;$ $\Delta ABC\;$ is straightforward to construct.
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73582217
