Line through a Point in an Angle

Given a point P in the interior of angle C. Draw a line through P that cuts off the angle a triangle of minimum area.

Solution

Given a point P in the interior of angle C. Draw a line through P that cuts off the angle a triangle of minimum area.

Reflect angle C in P (which produces two lines through the reflection C' of C parallel to the sides of angle C) and let A and B be the points of intersection of the pairs of lines.

Obviuosly, CAC'B is a parallelogram with P the midpoint of the diagonal CC'. It is then also the midpoint of the diagonal AB so that AB passes through P. We claim that ΔABC solves the problem at hand.

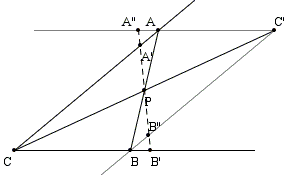
Indeed, let A'B' be another line through P. A'B' intersects AC' in A'' and BC' in B''. Now, since Area(CA'B') = Area(C'A''B''),

	Area(CA'B')	= (Area(CAC'B) + Area(AA'A'') + Area(BB'B'')) / 2
		= Area(CAB) + (Area(AA'A'') + Area(BB'B'')) / 2
		≥ Area(CAB),

with the equality only when A = A' = A'' and B = B' = B''.

Note: This problem relates to the problem of finding the triangle of minimum area that encloses a unit square. The sought triangle has the area of 2.

References

V. V. Prasolov, Problems in Planimetry II, Nauka, 1986, (16.15)

71543121