Pleasant Proportions in Triangle
Through an arbitrary point inside a triangle, three lines parallel to the sides of the triangle are drawn. They divide the sides into three segments each, whose lengths are shown below:
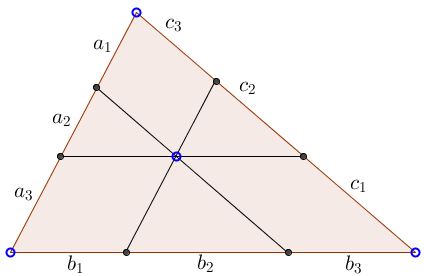
Prove that
$a_1b_1c_1=a_2b_2c_2=a_3b_3c_3.$
Proof
A simple proof is based on an observation that the three lines split the base triangle into three parallelograms and three similar triangles :
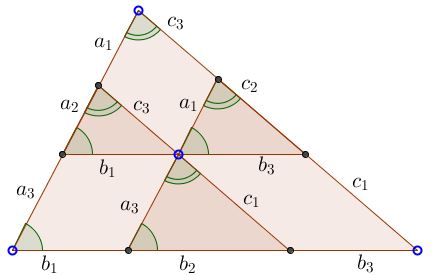
From several proportions due to the similarities I choose two:
$\displaystyle\frac{b_2}{c_1}=\frac{b_3}{c_2}$ and $\displaystyle\frac{b_1}{a_2}=\frac{b_3}{a_1}.$
The first is equivalent to $b_2c_2=c_1b_3$ into which we substitute $\displaystyle b_3=\frac{b_1a_1}{a_2}$ from the second:
$\displaystyle b_2c_2=c_1\frac{a_1b_1}{a_2}$
which is equivalent to $a_2b_2c_2=a_1b_1c_1.$ The second identity is proved similarly.
Acknowledgment
The problem has been offered at the 1990 USSR mathematical olympiad for grade 9 (B. Chinik, Kishinev.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73580633
