Relation Engendered By Medians
The medians $AM,$ $BN,$ $CP$ divide $\Delta ABC$ into six smaller ones as shown:
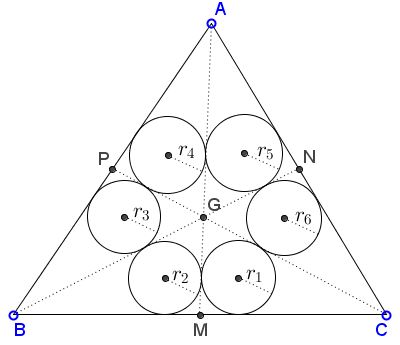
Prove that, for the inradii $r_1, \ldots, r_6$ of the small triangles, the following relation holds:
$\displaystyle\frac{1}{r_1}+\frac{1}{r_3}+\frac{1}{r_5}=\frac{1}{r_2}+\frac{1}{r_4}+\frac{1}{r_6}.$
Proof 1
The perimeter $p_1$ of $\Delta CGM$ equals
$p_1=CG+GM+CM=\displaystyle\frac{2}{3}m_{c}+\frac{1}{3}m_{a}+\frac{1}{2}a=\frac{1}{6}(4m_{c}+2m_{a}+3a).$
It follows that $\displaystyle\frac{1}{r_1}=\frac{1}{12}\frac{4m_{c}+2m_{a}+3a}{S_1}.$ However, note that all six small triangles have the same area which we'll denote $S.$ Then
$\displaystyle\frac{1}{r_1}=\frac{1}{12}\frac{4m_{c}+2m_{a}+3a}{S}.$
By the same token,
$\displaystyle\frac{1}{r_3}=\frac{1}{12}\frac{4m_{b}+2m_{c}+3c}{S}.$
and
$\displaystyle\frac{1}{r_5}=\frac{1}{12}\frac{4m_{a}+2m_{b}+3b}{S}$
such that
$\displaystyle\frac{1}{r_1}+\frac{1}{r_3}+\frac{1}{r_5}=\frac{1}{4}\frac{2(m_{a}+m_{b}+m_{c})+(a+b+c)}{S}.$
This being a symmetric expression in $a,b,c,$ we also have
$\displaystyle\frac{1}{r_2}+\frac{1}{r_4}+\frac{1}{r_6}=\frac{1}{4}\frac{2(m_{a}+m_{b}+m_{c})+(a+b+c)}{S}.$
Proof 2
We denote by $d_a$ the distances from $B$ and $C$ to $AM$ (which are of course equal), $k_a$ the distances from $P$ and $N$ to $AM$ (they which are also equal). $d_b,$ $d_c,$ and $k_b,$ $k_c$ are defined similarly. Then, for example, in $\Delta CGM,$
$\displaystyle r_1p_1=2S=\frac{1}{3}h_aCM=GM\cdot d_a=CG\cdot k_c.$
From this we obtain
$\displaystyle \frac{1}{r_1}=\frac{p_1}{2S}=\frac{3}{h_a}+\frac{1}{d_a}+\frac{1}{k_c}.$
Similar expressions hold for $\displaystyle \frac{1}{r_3}$ and $\displaystyle \frac{1}{r_5},$ with the sum of the three a symmetric expression in $a,b,c,$ proving that for the even indices the result is exactly the same.
Acknowledgment
The problem that is due to Gustavo Jimmy Garcia Paytan (Peru) was communicated to me along with the two proofs by Leo Giugiuc (Romania). The proofs are by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc, a Romanian crew.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573686
