An Inequality In Triangle and Without II
Problem
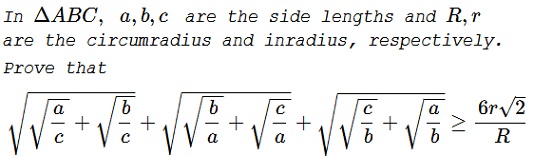
Remark
All solvers have observed that, due to Euler's inequality $R\ge 2r,\,$ $\displaystyle\frac{6r\sqrt{2}}{R}\le 3\sqrt{2},\,$ and went on to prove
$\displaystyle \sqrt{\sqrt{\frac{a}{c}}+\sqrt{\frac{b}{c}}}+\sqrt{\sqrt{\frac{b}{a}}+\sqrt{\frac{c}{a}}}+\sqrt{\sqrt{\frac{c}{b}}+\sqrt{\frac{a}{b}}}\ge3\sqrt{2}.$
Thus, this is the inequality that is proved below without additional comments. All solutions employ the AM-GM inequality.
Solution 1
Set $\displaystyle \frac{a}{c}=x^2,\,$ $\displaystyle \frac{b}{c}=y^2,\,$ $\displaystyle \frac{b}{a}=z^2.\,$ The required inequality becomes $\displaystyle \sqrt{x+y}+\sqrt{z+\frac{1}{x}}+\sqrt{\frac{1}{y}+\frac{1}{z}}\ge 3\sqrt{2}.\,$ We have
$\displaystyle \begin{align} \sqrt{x+y}+\sqrt{z+\frac{1}{x}}+\sqrt{\frac{1}{y}+\frac{1}{z}}&\ge 3\sqrt[6]{\left(x+y\right)\left(z+\frac{1}{x}\right)\left(\frac{1}{y}+\frac{1}{z}\right)}\\ &\ge 3\sqrt[6]{2\sqrt{xy}\cdot 2\frac{\sqrt{z}}{\sqrt{x}}\cdot \frac{2}{\sqrt{yz}}}=3\sqrt{2}. \end{align}$
Solution 2
First off, for all $x,y,z\gt 0,$
$\begin{align} (\sqrt{x}+\sqrt{y}+\sqrt{z})^2&=x+y+z+2(\sqrt{xy}+\sqrt{yz}+\sqrt{zx})\\ &\ge x+y+z+2\cdot 3\cdot \sqrt[3]{sqrt{xy}\sqrt{yz}\sqrt{zx}}\\ &=x+y+z+6\sqrt[3]{xyz}. \end{align}$
Thus,
(1)
$(\sqrt{x}+\sqrt{y}+\sqrt{z})^2\ge x+y+z+6\sqrt[3]{xyz}.$
Set $\displaystyle x=\frac{u+v}{w},\,$ $\displaystyle y=\frac{v+w}{u},\,$ $\displaystyle z=\frac{w+u}{v}.\,$ Then (1) gives
$\displaystyle \begin{align} \left(\sum_{cycl}\frac{u+v}{w}\right)^2&\ge\sum_{cycl}\frac{u+v}{w}+6\sqrt[3]{\prod_{cycl}\frac{u+v}{w}}\\ &\ge \sum_{cycl}\frac{u+v}{w}+6\sqrt[3]{\frac{2\sqrt{uv}\cdot 2\sqrt{vw}\cdot 2\sqrt{wu}}{uvw}}\\ &=\sum_{cycl}\frac{u+v}{w}+6\sqrt[3]{8}\\ &=\frac{(u+v)(v+w)(w+u)}{uvw}-2+12\\ &\ge\frac{2\sqrt{uv}\cdot 2\sqrt{vw}\cdot 2\sqrt{wu}}{uvw}+10\\ &=8+10=18. \end{align}$
It follows that
(2)
$\displaystyle\sqrt{\frac{u+v}{w}}+\sqrt{\frac{v+w}{u}}+\sqrt{\frac{w+u}{v}} \ge 3\sqrt{2}.$
With $u=\sqrt{a},\,$ $v=\sqrt{b},\,$ $w=\sqrt{c},\,$ (2) becomes the required inequality.
Solution 3
$\displaystyle\begin{align} LHS &\ge 3\sqrt[3]{ \sqrt{\frac{\sqrt{a}+\sqrt{b}}{\sqrt{c}}}\cdot \sqrt{\frac{\sqrt{b}+\sqrt{c}}{\sqrt{a}}}\cdot \sqrt{\frac{\sqrt{c}+\sqrt{a}}{\sqrt{b}}}}\\ &=3\sqrt[6]{\frac{(x+y)(y+z)(z+x)}{xyz}},\,\text{where}\,x=\sqrt{a},\,\text{etc.}\\ &\ge 3\sqrt[6]{ \frac{ 2\sqrt{xy}\cdot 2\sqrt{yz}\cdot 2\sqrt{zx}}{xyz}}\\ &=3\sqrt[6]{8}=3\sqrt{2}. \end{align}$
Acknowledgment
This is a problem from the Romanian Mathematics Magazine; it was kindly communicated to me by Dan Sitaru, along with his solution (Solution 2). Solution 1 is by Seyran Ibrahimov; Solution 3 is by Soumava Chakraborty.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73578372
