IMO 2009, Problem 4

Problem 4 from the IMO 2009

Here is Problem 4 from the IMO 2009:

Let ABC be a triangle with AB = AC. The angle bisectors of ∠CAB and ∠ABC meet the sides BC and CA at D and E, respectively. Let K be the incentre of triangle ADC. Suppose that ∠BEK = 45°. Find all possible values of ∠CAB.

Solution

Solution by Vo Duc Dien
(Saturday July 18, 2009)
Dedicated to my teacher Nguyen Hoi

Extend CK to meet BE at H. H is the center of the incircle of triangle ABC. HM = HD.

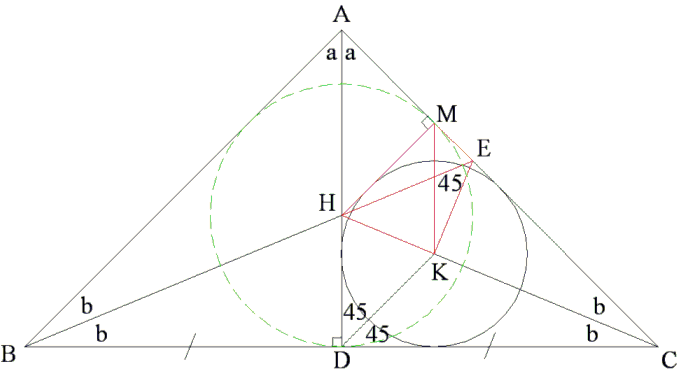
Since CH bisects ∠ACB, the two right triangles HDC and HMC are equal. Therefore ∠HMK = ∠HDK = 45°.

There are two possibilities: either M and E coincide or they are different. In the former case, BM is both the median and the altitude from B, implying BC = AB. Since also, AB = AC, all three sides in ΔABC are equal and the triangle is equilateral. Thus ∠CAB = 60°.

If M and E are distinct, we recall that ∠HEK = ∠BEK = 45°. Thus the quadrilateral HMEK is cyclic and, since ∠HME = 90°, HE serves as its diameter. It follows that ∠HKE is also right so that ∠KHE = 45°.

Further, ∠BHC = 180° - ∠KHE = 135°, 2b = 45°.

In triangle ABC we have ∠CAB = 180° - 4b = 90° which is the second possible value for ∠CAB.

72187072

Problem 4 from the IMO 2009

Solution by Vo Duc Dien (Saturday July 18, 2009) Dedicated to my teacher Nguyen Hoi

Solution by Vo Duc Dien
(Saturday July 18, 2009)
Dedicated to my teacher Nguyen Hoi