Problem 1 from the IMO 2006

Here is Problem 1 from the IMO 2006:

Let ABC be a triangle with incenter I. A point P in the interior of the triangle satisfies ∠PBA + ∠PCA = ∠PBC + ∠PCB. Show that AP ≥ AI, and that equality holds if and only if P = I.

The solution below is by Vo Duc Dien

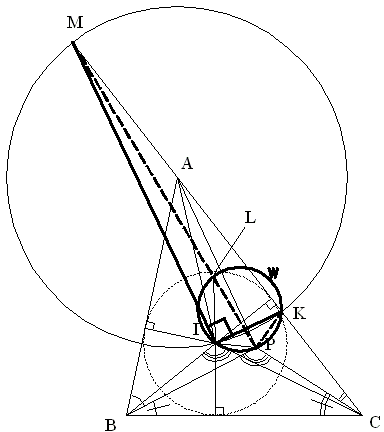
Chase the angles:

∠BIC = 180 - ½ (∠ABC + ∠ACB).

∠BPC = 180 - (∠PBC + ∠PCB).

The problem gives us

	∠PBA + ∠PCA	= ∠PBC + ∠PCB
		= ½ (∠ABC + ∠ACB).

Therefore, ∠BPC = ∠BIC.

Draw a circle with center at A that passes through point I and intersects AC at K.

(1)	∠MPK = 360° - ∠BPC - ∠MPB - ∠KPC

But

	∠BPC	= ∠BIC,
	∠MPB	= ∠MIB - ∠IMP - ∠IBP,
	∠KPC	= ∠KIC + ∠IKP + ∠ICP,
	∠IBP	= ½ ∠ABC - ∠PBC,
	∠ICP	= ∠PCB - ½ ∠ACB.

So that (1) becomes

	∠MPK	=	360° - ∠BIC - ∠MIB + ∠IMP + ∠IBP - ∠KIC - ∠IKP - ∠ICP
		=	360° - ∠BIC - ∠MIB + ∠IMP + ½∠ABC - ∠PBC - ∠KIC - ∠IKP + ½∠ACB - ∠PCB.

And since ½(∠ABC + ∠ACB ) = ∠PBC + ∠PCB,

	∠MPK	= (360° - ∠BIC - ∠MIB - ∠KIC) + ∠IMP - ∠IKP
	∠MIK	= 360° - ∠BIC - ∠MIB - ∠KIC
		= 90°
	∠MPK	= 90° + ∠IMP - ∠IKP
		= 90° + ∠IMP - ∠ILP

Further, ∠ILP > ∠IMP implies ∠IMP - ∠ILP < 0, or

∠MPK < 90°.

Therefore, point P is outside the circle with center A implying AP > AI.

(Note: a shorter solution is available elsewhere.)

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny