Further Arithmetic Progression in 30-60-90 Triangle
Problem
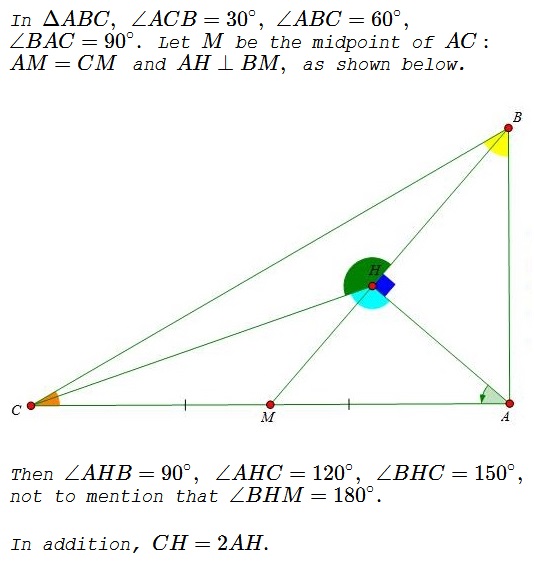
Solution
We have $AM^2=HM\cdot BM,\,$ implying $CM^2=MH\cdot MB,\,$ which means that $CM$ is tangent to the circumcircle $(BCH).$ It then follows, by the EAT and subsequent angle chasing, that
$\angle CHM=\angle CBH+\angle BCH=\angle HCM+\angle BCH=\angle BCM=30^{\circ}.$
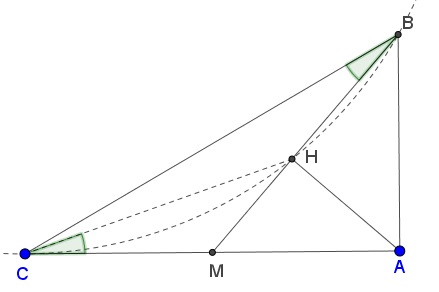
Thus, $\angle AHB=90^{\circ},$ $\angle AHC=120^{\circ},$ $\angle BHC=150^{\circ}.$
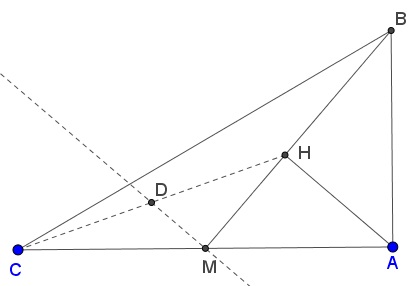
To prove $CH=2AH,$ let $D$ be on $CH$ such that $DM\parallel AH.$ Then $\Delta HDM$ is $30^{\circ}-60^{\circ}-90^{\circ}$ triangle so that $DH=2DM.$ But, by the construction, $2DM=AH\,$ and $2DH=CH,$ and the assertion follows.
Acknowledgment
The problem, with a solution, was kindly posted at the CutTheKnotMath facebook page by Nguyen Dung Thanh.
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73517699
