Van Khea's Fourth Identity in Triangle

Let $O$ be a point inside $\Delta ABC.$ Lines $AO,BO,CO$ cross the sides of the triangle at $D,E,F,$ as shown:

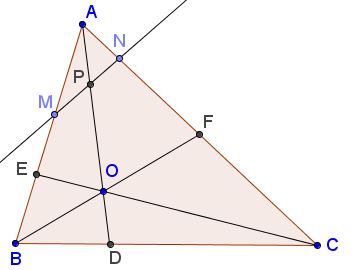
Van Khea's Fourth Identity in Triangle, problem

Line $MN,$ with $M\in AB$ and $M\in AC$ intersects $AD$ in $P.$ Prove that

(*)

$\displaystyle \frac{BM}{MA}\cdot\frac{AE}{EB}+\frac{CN}{NA}\cdot\frac{AF}{FC}=\frac{AO}{OD}\cdot\frac{DP}{PA}.$

(Note that in (*) and also below all segments are thought to be signed.)

The case $MN\parallel BC$ being trivial, we assume without loss of generality that $MN$ meets BC in $Q$ such that $B\in QC.$

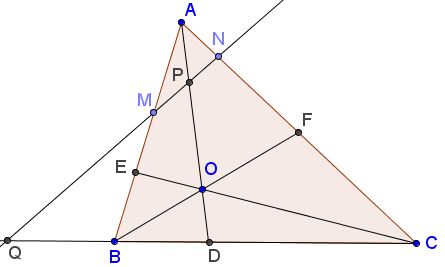
Van Khea's Fourth Identity in Triangle, problem

(1)

$\displaystyle\frac{AE}{EB}+\frac{AF}{FC}=\frac{AO}{OD}.$

By Menelaus' theorem in $\Delta ABD$ and the transversal $PMQ,$

(2)

$\displaystyle\frac{BM}{MA}=\frac{DP}{PA}\cdot\frac{QB}{QD}$

and in $\Delta ACD$ and the transversal $PNQ,$

(3)

$\displaystyle\frac{CN}{NA}=\frac{DP}{PA}\cdot\frac{QC}{QD}.$

Substituting (1-3) into (*) results in an equivalent identity:

$\displaystyle\frac{QB}{QD}\cdot\frac{AE}{EB}+\frac{QC}{QD}\cdot\frac{AF}{FC}=\frac{AE}{EB}+\frac{AF}{FC}$

which, in turn, can be transformed into

$\displaystyle\frac{AE}{EB}\cdot\frac{QB-QD}{QD}+\frac{AF}{FC}\cdot\frac{QC-QD}{QD}=0,$

or,

$\displaystyle\frac{AE}{EB}BD+\frac{AF}{FC}CD=0,$

which is equivalent to

$\displaystyle\frac{AE}{EB}\cdot\frac{BD}{DC}\cdot\frac{CF}{FA}=1.$

The latter is the Ceva condition for $\Delta ABC$ and the cevians through $O.$

The problem has been sent to me by Leo Giugiuc with credits to Van Khea. The proof is by Leo Giugiuc.

72354244