Centroids and Circumcenters
Problem
Sohail Farhangi
Submitted 9 October, 2015
Given $\triangle ABC$ with centroid $G$ and circumcenter $O$, construct the circumcenters of triangles $AGB, BGC,$ and $CGA$, which we will denote by $O_c, O_a,$ and $O_b$ respectively. Let the centroid of $\triangle O_aO_bO_c$ be $G'$. Show that $G'$ and $O$ coincide.
The proof depends on the following lemma.
Lemma
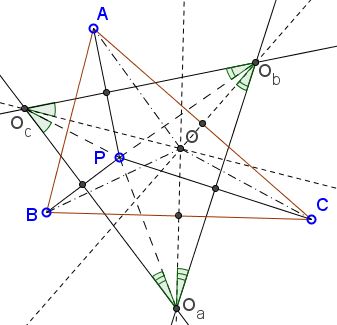
Proof of Lemma
Let $M_c$ be the midpoint of $AB$, and let $E$ be the midpoint of $BP$.
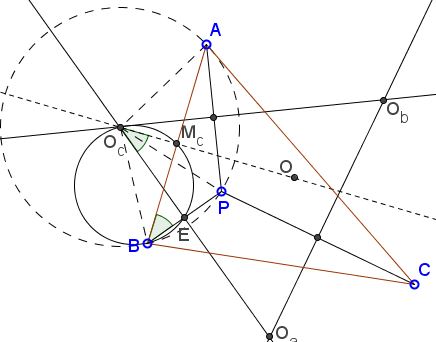
It can be seen that $O_cO_a \perp BP$ and $O_cO \perp AB$, so it follows that $O_cM_cEB$ is a cyclic quadrilateral, and that $\angle PBA = \angle EBM_c = \angle EO_cM_c = \angle O_aO_cO$. Furthermore, we have that $\displaystyle\angle PBA = \frac{\angle PO_cA}{2} = \angle PO_cO_b = O_aO_cO$. The argument can be repeated for vertices $O_b$ and $O_a$ to attain the desired result.
Proof of the main result
It is well known that the isogonal conjugate of the centroid, is the Lemoine point, hence using Lemma we only need to show that $G$ is the Lemoine point of $\triangle O_aO_bO_c$.
Since the trilinear coordinates of the Lemoine point are proportional to the sides of the triangle, it only remains to verify that $GD:GE:GF = O_bO_c:O_cO_a:O_aO_b$.
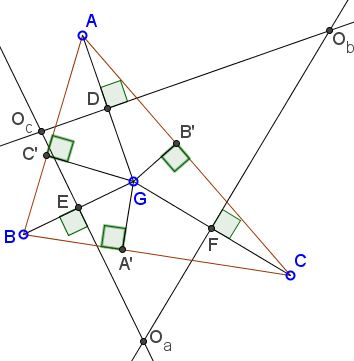
To see that this is so, let $A',$ $B',$ $C'$ be the projections of $G$ on $BC,$ $CA,$ $AB,$ respectively; $D,$ $E,$ $F$ are the projections on $O_bO_c,$ $O_cO_a,$ $O_aO_b.$ For, say $GD:GE,$ we have
$\displaystyle\begin{align} \frac{GD}{GE} &= \frac{GA}{GB}\\ &= \frac{GA}{GB}\cdot\frac{\sin(\angle GCB)}{\sin(\angle GCA)}\cdot \frac{\sin(\angle GCA)}{\sin(\angle GCB)}\\ &= \frac{GA}{\sin(\angle GCA)}\cdot \frac{\sin(\angle GCB)}{GB}\cdot \frac{\sin(\angle GCA)}{\sin(\angle GCB)}\\ &= \frac{AC}{\sin(\angle AGC)}\cdot \frac{\sin(\angle BGC)}{BC}\cdot \frac{\sin(\angle GCA)}{\sin(\angle GCB)}\\ &= \frac{AC}{BC}\cdot \frac{GC\cdot \sin(\angle GCA)}{GC\cdot \sin(\angle GCB)}\cdot \frac{\sin(\angle BGC)}{\sin(\angle AGC)}\\ &= \frac{AC}{BC}\cdot \frac{GB'}{GA'}\cdot \frac{\sin(\angle BGC)}{\sin(\angle AGC)}= \frac{[\Delta AGC]}{[\Delta BGC]}\cdot \frac{\sin(\angle BGC)}{\sin(\angle AGC)}\\ &= \frac{\sin(\angle BGC)}{\sin(\angle AGC)}= \frac{\sin(\angle EO_aF)}{\sin(\angle DO_bF)}= \frac{\sin(\angle O_cO_aO_b)}{\sin(\angle O_aO_bO_c)}\\ &= \frac{O_bO_c}{O_cO_a}. \end{align}$
Repeating the argument to evaluate $\displaystyle\frac{GE}{GF}=\frac{O_cO_a}{O_aO_b}$ attains the desired result.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579889
