Angle in Square
Source
The following problem has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. Miguel and Daniel Hardisky have posted practically identical solutions. The one below is due to Daniel.
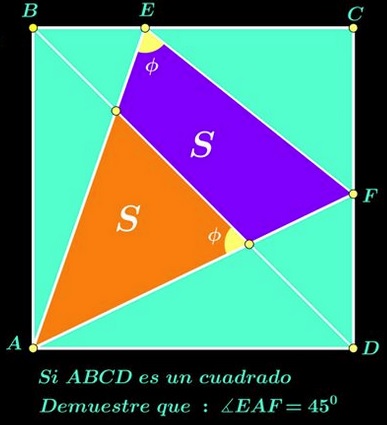
Problem
In square $ABCD,$ point $E$ is on side $BC,$ point $F$ on $CD.$ Points $P$ and $Q$ are the intersections of the diagonal $BD$ with $AE$ and $AF,$ respectively. It is known that $\angle AEF=\angle AQB$ and that the area $[PEFQ]$ of the quadrilateral $PEFQ$ equals that of $\Delta APQ.$

Prove that $\angle PAQ=45^{\circ}.$
Note that a converse problem is considered elsewhere.
Proof
Assume the side of the square equals $1.$ Since $\angle AEF=\angle APB$ and triangles $APQ$ and $AFE$ share the angle at $A$ they are similar. It is also given that their areas are in the ratio $1:2,$ $[\Delta AFE]/[\Delta APQ]=2.$

Drop the altitudes $AM$ and $AN$ and note that $AM^{2}/AN^{2}=[\Delta AFE]/[\Delta APQ]=2$ and that $AN$ is half the diagonal $AC$ of the square so that $AN=\sqrt{2}/2.$ From this it follows that $AM=1,$ implying that, as right triangles, $\Delta ADF=\Delta AMF$ and $\Delta ABE=\Delta AME.$ It follows that $\angle BAE=\angle MAE$ and $\angle DAF = \angle MAF$ so that
$\angle BAD = 2(\angle MAE +\angle MAF) = 2\angle EAF.$
Thus, indeed, $\angle EAF = 45^{\circ}.$
Extras
The configuration has additional properties. Two can be shown by simple angle chasing.
$EQ\perp AF$ and $FP\perp AE.$
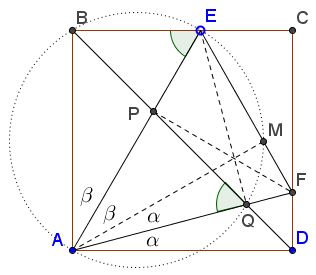
Indeed, $\angle AEB=90^{\circ}-\beta=\angle AEM=\angle AQP,$ implying $Q\in (ABE),$ a circle with diameter $AE.$ Thus $\angle AQE=90^{\circ}.$ Similarly, $FP\perp AE.$
$C\in (PEFQ).$
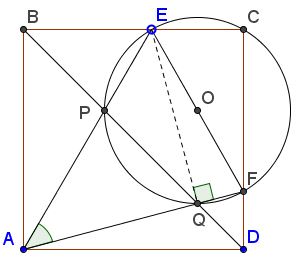
Indeed, $\angle EQF=90^{\circ},$ making $EF$ a diameter of $(PEFQ).$ Since, $\angle ECF=90^{\circ},$ $C\in (PEFQ).$
More accurately,
In square $ABCD,$ point $E$ is on side $BC,$ point $F$ on $CD.$ Points $P$ and $Q$ are the intersections of the diagonal $BD$ with $AE$ and $AF,$ respectively. Then $P,Q\in (ECF)$ iff $\angle EAF=45^{\circ}.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73574052
